AVDDPG – Federated reinforcement learning applied to autonomous platoon control
Abstract
Since 2016 federated learning (FL) has been an evolving topic of discussion in the artificial intelligence (AI) research community. Applications of FL led to the development and study of federated reinforcement learning (FRL). Few works exist on the topic of FRL applied to autonomous vehicle (AV) platoons. In addition, most FRL works choose a single aggregation method (usually weight or gradient aggregation). We explore FRL's effectiveness as a means to improve AV platooning by designing and implementing an FRL framework atop a custom AV platoon environment. The application of FRL in AV platooning is studied under two scenarios: (1) Inter-platoon FRL (Inter-FRL) where FRL is applied to AVs across different platoons; (2) Intra-platoon FRL (Intra-FRL) where FRL is applied to AVs within a single platoon. Both Inter-FRL and Intra-FRL are applied to a custom AV platooning environment using both gradient and weight aggregation to observe the performance effects FRL can have on AV platoons relative to an AV platooning environment trained without FRL. It is concluded that Intra-FRL using weight aggregation (Intra-FRLWA) provides the best performance for controlling an AV platoon. In addition, we found that weight aggregation in FRL for AV platooning provides increases in performance relative to gradient aggregation. Finally, a performance analysis is conducted for Intra-FRLWA versus a platooning environment without FRL for platoons of length 3, 4 and 5 vehicles. It is concluded that Intra-FRLWA largely out-performs the platooning environment that is trained without FRL.
Keywords
1. INTRODUCTION
In recent years, federated learning (FL) and its extension federated reinforcement learning (FRL) have become a popular topic of discussion in the artificial intelligence (AI) community. The concept of FL was first proposed by Google with the development of the federated averaging (FedAvg) aggregation method [1]. FedAvg provided an increase in the performance of distributed systems while also providing privacy advantages when compared to centralized architectures for supervised machine learning (ML) tasks [1-3]. FL's core ideology was initially motivated by the need to train ML models from distributed data sets across mobile devices while minimizing data leakage and network usage [1].
Research on the topics of reinforcement learning (RL) and deep reinforcement learning (DRL) has made great progress over the years; however, there remain important challenges for ensuring the stable performance of DRL algorithms in the real world. DRL processes are often sensitive to small changes in the model space or hyper-parameter space, and as such the application of a single trained model across similar systems often leads to control inaccuracies or instability [4,5]. In order to overcome the stability challenges that DRL poses, often a model must be manually customized to accommodate the finite differences amongst similar agents in a distributed system. FRL aims to overcome the aforementioned issues by allowing agents to share private information in a secure way. By utilizing an aggregation method, such as FedAvg [1], systems with many agents can have decreased training times with increased performance.
Despite the popularity of FL and FRL, to the best of our knowledge at the time of this study, there are no works applying FRL to platoon control. In general, there are two types of "models" for AV decision making: vehicle-following modeling and lane-changing modeling [6]. For the purposes of this study, the vehicle-following approach known as co-operative adaptive cruise control (CACC) is explored. Vehicle following models are based on following a vehicle on a single lane road with respect to a leading vehicle's actions [7]. CACC is a multi-vehicle control strategy where vehicles follow one another in a line known as a platoon, while simultaneously transmitting vehicle data amongst each other [8]. CACC platoons have been proven to improve traffic flow stability, throughput and safety for occupants [8,9]. Traditionally controlled vehicle following models have limited accuracy, poor generalization from a lack of data, and a lack of adaptive updating [7].
We are motivated by the current state-of-the-art for CACC AV Platoons, along with previous works related to FRL, to apply FRL to the AV platooning problem and observe the performance benefits it may have on the system. We propose an FRL framework built atop a custom AV platooning environment in order to analyse FRL's suitability for improving AV platoon performance. In addition, two approaches are proposed for applying FRL amongst AV platoons. The first proposed method is inter-platoon FRL (Inter-FRL), where FRL is applied to AVs across different platoons. The second proposed method is intra-platoon FRL (Intra-FRL), where FRL is applied to AVs within the same platoon. We investigate the possibility of Inter-FRL and Intra-FRL as a means to increase performance using two aggregation methods: averaging model weights and averaging gradients. Furthermore, the performance of Inter-FRL and Intra-FRL using both aggregation methods is studied relative to platooning environments trained without FRL (no-FRL). Finally, we compare the performance of Intra-FRL with weight averaging (Intra-FRLWA) against a platooning environment trained without FRL for platoons of length 3, 4 and 5 vehicles.
1.1. Related works
In this subsection, the current state-of-the-art is presented for FRL and DRL applied to AV's. In addition the contributions of this paper are presented.
1.1.1. Federated reinforcement learning
There are two main areas of research in FRL currently: horizontal federated reinforcement learning (HFRL), and vertical federated reinforcement learning (VFRL). HFRL has been selected as the algorithm of choice for the purposes of this study. HFRL and VFRL differ with respect to the structure of their environments and aggregation methods. All agents in an HFRL architecture use isolated environments. It follows that each agent's action in an HFRL system has no effect on the other agents in the system. An HFRL architecture proposes the following training cycle for each agent: first, a training step is performed locally, second, environment specific parameters are uploaded to the aggregation server, and lastly, parameters are aggregated according to the aggregation method and returned to each agent in the system for another local training step. HFRL may be noted to have similarities to "Parallel RL". Parallel RL is a long studied field of RL, where agent gradients are transferred amongst each other [5,10,11].
Reinforcement learning is often a sequential learning process, and as such data is often non-IID with a small sample space [12]. HFRL provides the ability to aggregate experience while increasing the sample efficiency, thus providing more accurate and stable learning [13]. Some of the current works applying HFRL to a variety of applications are summarized below.
A study by Lim et al. aims to increase the performance of RL methods applied to multi-IoT device systems. RL models trained on single devices are often unable to control devices in a similar albeit slightly different environment [5]. Currently, multiple devices need to be trained separately using separate RL agents [5]. The methods proposed by Lim et al. sped up the learning process by 1.5 times for a two agent system. In a study by Nadiger et al., the challenges in the personalization of dialogue managers, smart assistants and more are explored. RL has proven to be successful in practice for personalized experiences; however, long learning times and no sharing of data limit the ability for RL to be applied at scale. Applying HFRL to atari non-playable characters in pong showed a median improvement of 17% for the personalization time [10]. Lastly, Liu et al. discuss RL as a promising algorithm for smart navigation systems, with the following challenges: long training times, poor generalization across environments, and storing data over long periods of time [14]. In order to address these problems, Liu et al. proposed the architecture 'Lifelong FRL', which can be categorized as an HFRL problem. It is found the Lifelong FRL increased the learning rate for smart navigation system when tested on robots in a cloud robotic system [14].
The successes of the FedAvg algorithm as a means to improve performance and training times for systems have inspired further research into how aggregation methods should be applied. The design of the aggregation method is crucial in providing performance benefits to that of the base case where FRL is not applied. The FedAvg [3] algorithm proposed the averaging of gradients in the aggregation method. In contrast, Liang et al. proposed using model weights in the aggregation method for AV steering control [15]. Thus, FRL applications can differ based upon the selection of which parameter to use in the aggregation method. A study by Zhang et al. explores applying FRL to a decentralized DRL system optimizing cellular vehicle-to-everything communication[16]. Zhang et al. utilize model weights in the aggregation method, and describe a weighting factor dividing the sum batch size for all agents by the training batch size for a specific agent[16]. In addition, the works of Lim et al. explore how FRL using gradient aggregation can improve convergence speed and performance on the OpenAI-gym environments CartPole-V0, MountainvehicleContinuous-V0, Pendulum-V0 and Acrobot-V1 [17]. Lim et al. determined that aggregating gradients using FRL creates high performing agents for each of the OpenAI-gym environments relative to models trained without FRL[17]. In addition, Wang et al. apply FRL to heterogeneous edge caching [18]. Wang et al. show the effectiveness of FRL using weight aggregation to improve hit rate, reduce average delays in the network and offload traffic[18]. Lastly, Huang et al. apply FRL using model weight aggregation to Service Function Chains in network function virtualization enabled networks[19]. Huang et al. observe that FRL using model weight aggregation provides benefits to convergence speed, average reward and average resource consumption[19].
Despite the differences in FRL applications within the aforementioned studies, each study maintains a similar goal: to improve the performance of each agent within the system. None of the aforementioned works explore the differences in whether gradient or model weight aggregation is favourable in performance, and many of the works apply FRL to distributed network or communications environments. It is the goal of this study to conclude whether model weight or gradient aggregation is favourable for AV platooning, as well as be one of the first (if not the first) to apply FRL to AV platooning.
1.1.2. Deep reinforcement learning applied to AV platooning
In recent years, there has been a surge in autonomous vehicle (AV) research, likely due to the technologies potential for increasing road safety, traffic throughput and fuel economy [6,20]. Two areas of research are often considered when delving into an AV model: supervised learning or RL [20]. Driving is considered a multi-agent interaction problem, and due to the large variability of road data, it can be quite challenging (or near impossible) to gather a data set variable enough to train a supervised model [21]. Driving data is collected from humans, which can also limit an AI's ability to that of human level [6]. In contrast, RL methods are known to generalize quite well [20]. RL approaches are model-free and a model may be inferred by the algorithm while training.
In order to improve the limitations of vehicle following models, DRL has been a steady area of research in the AV community, with many authors contributing works to DRL applied to CACC [8,9,22,23]. In a study by Lin et al., a DRL framework is designed to control a CACC AV platoon[22]. The DRL framework uses the deep deterministic policy gradient (DDPG) [24] algorithm and is found to have near-optimal performance [22]. In addition, Peake et al. identify limitations in platooning with regard to the communication in platooning[23]. Through the application of a multi-agent reinforcement learning process, i.e. a policy gradient RL and LSTM network, the performance of a platoon containing 3-5 vehicles is improved upon that of current RL applications to platooning [23]. Furthermore, Model Predictive Control (MPC) is the current state-of-the-art for real-time optimal control practices [25]. The study performed by Lin et al. applies both MPC and DRL methodologies to the AV platoon problem, observing a DRL model trained using the DDPG algorithm produces merely a 5.8% episodic cost higher than the current state-of-the-art[25]. The works of Yan et al. propose a hybrid approach to the AV platooning problem where the platoon is modeled as a Markov Decision Process (MDP) in order to collect two rewards from the system at each time step simultaneously[26]. This approach also incorporates jerk, the rate of change of acceleration in the calculation of the reward for each vehicle in order to ensure passenger comfort [26]. The hybrid strategy led to increased performance to that of the base DDPG algorithm, as the proposed framework switches between using classic CACC modeling and DDPG depending on the performance degradation of the DDPG algorithm [26]. In another study by Zhu et al., a DRL model is formulated and trained using DDPG to be evaluated against real world driving data. Parameters such as time to collision, headway, and jerk were considered in the DRL model's reward function[27]. The DDPG algorithm provided favourable performance to that of the analysed human driving data, with regard to more efficient driving via reduced vehicle headways, and improved passenger comfort with lower magnitudes of jerk[27]. As Vehicle-to-Everything (V2X) communications are envisioned to have a beneficial impact on the performance of platoon controllers, the works of Lei et al. investigates the value of V2X communications for DRL-based platoon controllers. Lei et al. emphasizes the trade-off between the gain of including exogenous information in the system state for reducing uncertainty and the performance erosion due to the curse-of-dimensionality[28].
When formulating the AV platooning problem as a DRL model DDPG is prominently selected as the algorithm for training. DDPG's ability to handle continuous actions space and complex state's is perfect for the CACC platoon problem. However, despite the DDPG algorithm's success in literature, there are still instability challenges related to the algorithm along with a time consuming hyper-parameter tuning process to account for the minute differences in vehicle models/dynamics amongst platoons. As previously discussed, FRL provides advantages in these areas where information sharing can accelerate performance during training and improve the performance of the system as a whole. In addition, the ability to share experience across like models has been proven to allow for fast convergence of models, which further optimizes the performance of DDPG when applied to AV platoons [5].
1.2. Contributions
To the best of our knowledge, no works at the time of this study existed covering the specific topic of FRL applied to platoon control. Many of the works existing on FRL have shown the benefits of FRL with regard to the increased rate of convergence and overall system performance with distributed networks, edge caching and communications [16-19]. Furthermore, of the works cited in this study, the works closely related to FRL for platoon control are those of Peake et al. and Liang et al.[15,23]. In contrast to Liang et al., where FedAvg is applied successfully to control the steering angle of a single vehicle, we apply FRL to an AV platooning problem where the control of multiple vehicles' positions and spacing are required [15]. Peake et al. explore multi-agent reinforcement learning and its ability to improve the performance of AV platoons experiencing communication delays[23]. Although Peake et al. are also successful in their approach, there is no specific reference to FRL in the paper[23]. In addition, a variety of existing works on FRL choose to use either gradients or model weights in the FRL aggregation method. This study explores how both aggregation methods can provide benefits to the AV platooning problem and, most importantly, which provides a better result. Finally, this study further distinguishes its approach from existing literature by declaring two possible ways to apply FRL to AV platooning:
In contrast to existing literature, where it is common to average the parameters across each model in the system, for Intra-FRL, we propose a directional averaging where follower vehicles incorporate the preceding vehicle parameters in the computation of the gradients or weights. Thus, in Intra-FRL, the leading vehicle trains independently of those following. The AV platoon provides a unique playground environment suitable for exploring the suitability of FRL as a means to increase the performance of systems with regard to convergence rate and performance.
2. PROPOSED FRAMEWORK
In this section, a state space model is formulated and presented for the AV platooning problem. Next, the MDP model is presented, outlining the platoon system's state space, action space and reward function. Lastly, the FRL DDPG algorithm design and application to AV platooning are described.
2.1. CACC CTHP model formulation
Consider a platoon
As illustrated in Figure 1,for a general vehicle (
The headway
In addition, the desired headway
where
Therefore, the state of
The state space formula for
where
2.2. MDP model formulation
The AV platooning problem can be formulated as an MDP problem, where the optimization objective is to minimize the previously defined
2.2.1. State space
The state space formula (6) can be discretized using the forward euler method giving the system equation below
where
2.2.2. Action space
Each vehicle within a single lane platoon follows the vehicle in front of it, and as such the only action the vehicle may take to maintain a desired headway is to accelerate, or decelerate. The action for the system is defined as the control input
2.2.3. Reward function
The design of a reward in a DDPG system is critical to providing good performance within the system. In the considered driving scenario, it is logical to minimize position error, velocity error, the amount of time spent accelerating and the jerkiness of the driving motion. The proposed reward thus includes the normalized position error,
2.3. FRL DDPG algorithm
In this section, the design for implementing the FRL DDPG algorithm on the AV platooning problem is presented.
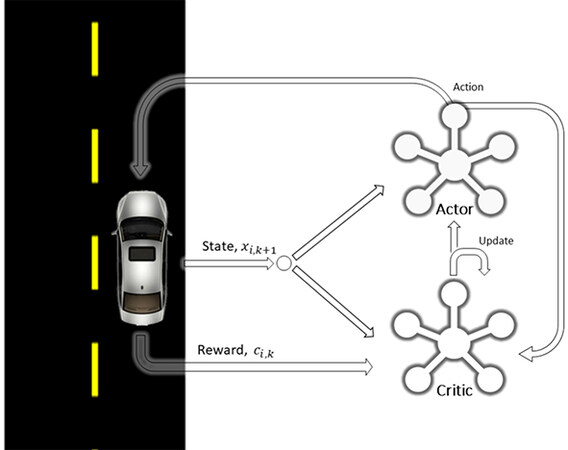
2.3.1. DDPG model description
The DDPG algorithm is composed of an actor,
2.3.2. Inter and intra FRL
Modifications to the base DDPG algorithm are needed in order to implement Inter-FRL and Intra-FRL. In order to implement FedAvg the following modifications are required:
In order to perform FRL, it has been proven that including an update delay between global FRL updates is beneficial for performance [5]. In addition, turning off FRL partway through training is important to allow each agent to refine their models independently of each other such that they can perform best with respect to their environments [5]. Lastly, it has also been shown that global updates and local updates should not be performed in the same episode [15].
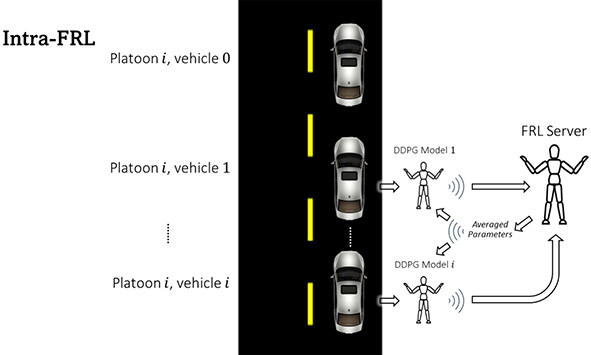
Two methods of aggregation are implemented in the system design, Inter-FRL (see Figure 3), and Intra-FRL (see Figure 4). The proposed system is capable of aggregating both the model weights and gradients for each model so that either type of parameter may be averaged for use in global updates. The FRL server has the responsibility of averaging the parameters (model weights or gradients) across each agent in the system.
The pseudo-code for the Inter/Intra-FRL algorithm is presented in Algorithm 1. The system is designed to allow the training of any number of equal length platoons. At the lowest level, a DDPG agent exists for each vehicle in each platoon. As such, a DRL model must be initialized for each vehicle in the whole system. Each DDPG agent trains separately from the others before data is uploaded to the FRL server. Federated averaging is applied at a given time delay known as the FRL update delay, while being terminated at a given episode as defined by the cutoff ratio as seen in Table 3. Currently, Algorithm 1 is synchronous, and the FRL server is also synchronous.
Algorithm 1: FRL applied to an AV platoon. 
3. EXPERIMENTAL RESULTS
In this section, the experimental setup for applying both Inter and Intra-FRL to the AV platooning environment is presented. The AV platooning environment and Inter/Intra FRL algorithms are implemented in Python 3.7 using Tensorflow 2.
3.1. Experimental setup
The parameters specific to the AV platoon environment are summarized in Table 1. The time step interval is
Parameters of the AV platoon environment
| Parameter | Value |
| Time step | 0.1 s |
| Number of time steps per training episode | 600 |
| Time gap | 1 s |
| Driveline dynamics coefficient | 0.1 s |
| Maximum absolute control input | 2.5 |
| Reward coefficient | 0.4 |
| Reward coefficient | 0.2 |
| Reward coefficient | 0.2 |
| Reward coefficient | 0.2 |
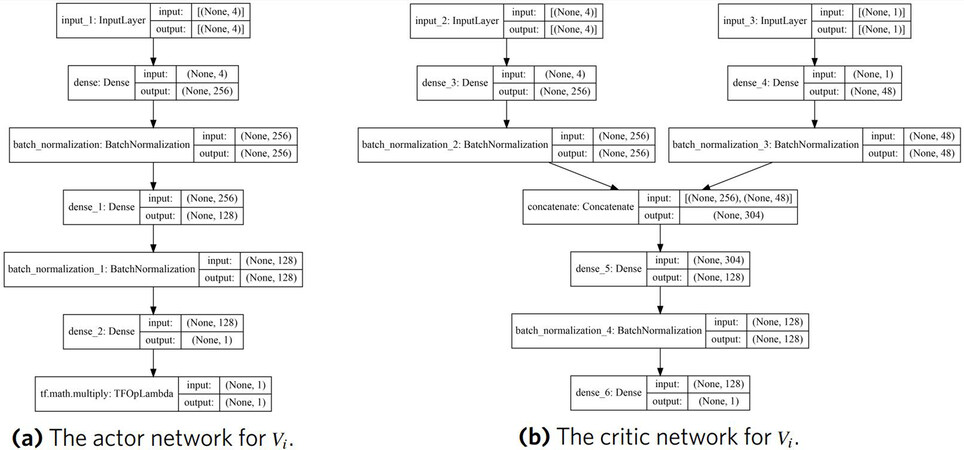
Each DDPG agent consists of a replay buffer, and networks for the actor, target actor, critic and target critic. The actor network contains four layers: an input layer for the state, two hidden layers with 256 and 128 nodes, respectively, and an output layer. Both hidden layers use batch normalization and the relu activation function. The output layer uses the tanh() activation function. The output layer is scaled by the high bound for the control output, in this case 2.5
Hyperparameters for the DDPG Algorithm
| Hyperparameter | Value |
| Actor learning rate | 5e-05 |
| Critic learning rate | 0.0005 |
| Batch size | 64 |
| Noise | Ornstein-Uhlenbeck Process with |
| Weights and Biases | random uniform distribution |
| Initialization |
The hyperparameters specific to Inter and Intra-FRL are presented in Table 3. During a training session with FRL, both local updates and FRL updates with aggregated parameters are applied to each DDPG agent in the system. FRL updates usually occur at a given frequency known as the FRL update delay, and furthermore, FRL updates may be terminated at a specific training episode as defined by the FRL cutoff ratio. The FRL update delay is defined as the time in seconds between FRL updates during a training episode. The FRL cutoff ratio is the ratio of the number of episodes where FRL updates are applied divided by the total number of episodes in a training session. Note that the aggregation method denotes whether the model gradients or weights are averaged during training using FRL.
For the purposes of this study, an experiment is defined as a training session for a specific configuration of hyper-parameters, using the algorithm defined in Algorithm 1. During each experiment training session, model parameters were trained through the base DDPG algorithm or FRL in accordance with Algorithm 1. Once training has concluded, a simulation is performed using a custom built evaluator API. The evaluator performs simulations for a single 60 second episode using the trained models, calculating the cumulative reward of the model(s) in the experiment. The entire project is designed and implemented using Python3, and Tensorflow. As previously stated, each vehicle in the platoon is modelled using the CACC CTHP model described in Section 3. For the purposes of this study, multiple sets of DRL experiments were conducted, using 4 random seeds (1-4) for training and a single random seed (6) across all evaluations.
3.2. Inter-FRL
In order to evaluate the effectiveness of Inter-FRL relative to the base case where a DRL model is trained using DDPG without FRL, 4 experiments are conducted without Inter-FRL (no-FRL), and 8 with. For each of the 12 conducted experiments, 2 platoons with 2 vehicles each were trained using one of the four random seeds. Once training across the four seeds has completed, the cumulative reward for a single evaluation episode is evaluated. For the experiments using Inter-FRL, two aggregation methods are examined. First, the gradients of each model are averaged during training, and second, the model weights are averaged. The multi platoon system trains and shares the aggregated parameters (gradients or weights) amongst vehicles with the same index across platoons. The federated server is responsible for performing the averaging, and each vehicle performs a training episode with the averaged parameters in addition to their local training episodes in accordance with the FRL update delay and FRL cutoff ratio (see Table 3). Note that here-after Inter-FRL with gradient aggregation is denoted Inter-FRLGA, and Inter-FRL with weight aggregation is denoted Inter-FRLWA.
FRL Specific Initial Hyperparameters
| FRL type | Aggregation method | Hyperparmeter | Value |
| Inter-FRL | Gradients | FRL update delay | 0.1 |
| Inter-FRL | Gradients | FRL cutoff ratio | 0.8 |
| Inter-FRL | Weights | FRL update delay | 30 |
| Inter-FRL | Weights | FRL cutoff ratio | 1.0 |
| Intra-FRL | Gradients | FRL update delay | 0.4 |
| Intra-FRL | Gradients | FRL cutoff ratio | 0.5 |
| Intra-FRL | Weights | FRL update delay | 0.1 |
| Intra-FRL | Weights | FRL cutoff ratio | 1.0 |
3.2.1. Performance across 4 random seeds
The performance for each of the systems is calculated by averaging the cumulative reward of each vehicle in the 2 vehicle 2 platoon system, as summarized in Table 4. For each of the 3 cases (base case, Inter-FRLGA and Inter-FRLWA), training sessions were run using 4 random seeds. In order to determine the highest performing system overall, an average and standard deviation is obtained from the result of training using the 4 random seeds. From Table 4,it is observed that both Inter-FRL scenarios using gradient and weight aggregation provide large performance increases to that of the base case.
Performance after training across 4 random seeds. Each simulation result contains 600 time steps
| Training method | Seed 1 | Seed 2 | Seed 3 | Seed 4 | Average system reward | Standard deviation |
| No-FRL | -3.73 | -2.89 | -4.69 | -3.38 | -3.67 | 0.66 |
| Inter-FRLGA | -2.79 | -2.81 | -3.05 | -2.76 | -2.85 | 0.11 |
| Inter-FRLWA | -2.64 | -2.88 | -2.92 | -2.93 | -2.84 | 0.12 |
3.2.2. Convergence properties
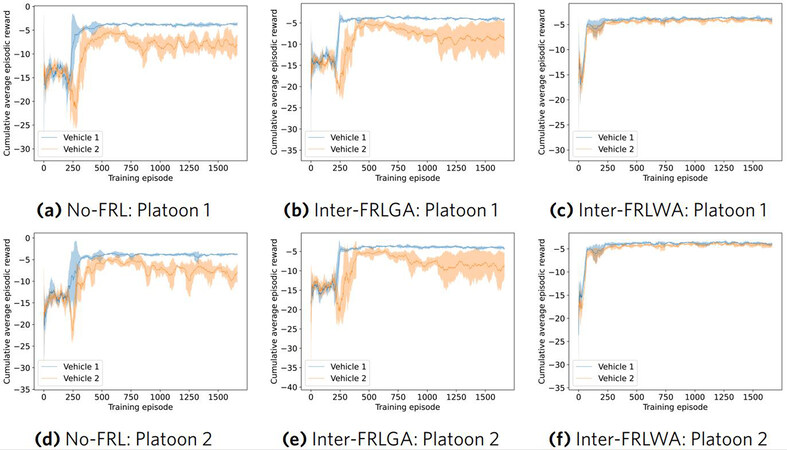
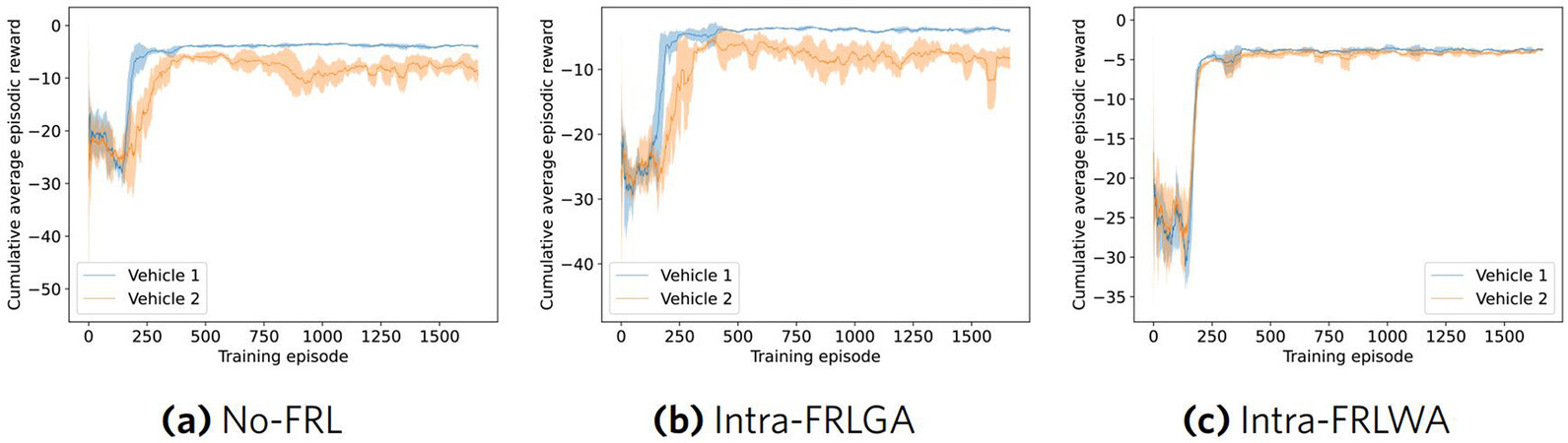
The cumulative reward is calculated over each training episode, and a moving average is computed over 40 episodes to generate Figure 6a-6f. It can be seen that the cumulative reward for Inter-FRLWA not only converges more rapidly than both no-FRL and Inter-FRLGA, but Inter-FRLWA also appears to have a more stable training session as indicated by the lower magnitude of the shaded area (the standard deviation across the four random seeds).
3.2.3. Test results for one episode
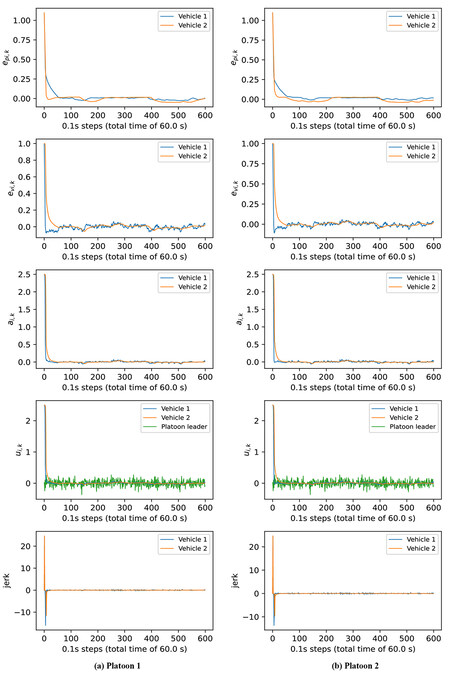
In Figure 7a and 7b,a simulation is performed over a single training episode plotting the jerk, along with the control input
3.3. Intra-FRL
In order to evaluate the effectiveness of Intra-FRL relative to the base AV platooning scenario, 4 experiments are conducted without Intra-FRL (no-FRL), and 8 with. For each of the conducted experiments, 1 platoon with 2 vehicles is trained using 4 random seeds. A single platoon is required for studying Intra-FRL as parameters are shared amongst vehicles within the platoon (no sharing is performed from vehicle's in one platoon to another). Once training across the four seeds is completed, the cumulative reward for a single evaluation episode is evaluated. Similar to the experiments using Inter-FRL, two aggregation methods are examined. First, the gradients of each model are averaged during training, and second, the model weights are averaged. The platoon trains and shares the aggregated parameters (gradients or weights) from vehicle to vehicle such that data is averaged and updated amongst vehicles within the same platoon. The federated server is responsible for performing the averaging, and each vehicle performs a training episode with the averaged parameters in addition to their local training episodes in accordance with the FRL update delay and FRL cutoff ratio (see Table 3). Note that here-after Intra-FRL with gradient aggregation is denoted Intra-FRLGA, and Intra-FRL with weight aggregation is denoted Intra-FRLWA.
3.3.1. Performance across 4 random seeds
The performance for the platoon is calculated by averaging the cumulative reward generated by the simulation for each of the 4 random seeds and is summarized in Table 5. The results in Table 5 summarize the performance for no-FRL, Intra-FRLGA, and lastly Intra-FRLWA. It is observed that Intra-FRLWA performs most favourably, followed by no-FRL and lastly Intra-FRLGA.
Performance after training across 4 random seeds. Each simulation result contains 600 time steps
| Training method | Seed 1 | Seed 2 | Seed 3 | Seed 4 | Average system reward | Standard deviation |
| No-FRL | -3.84 | -3.40 | -3.29 | -3.21 | -3.44 | 0.24 |
| Intra-FRLGA | -2.85 | -8.05 | -4.23 | -2.99 | -4.53 | 2.10 |
| Intra-FRLWA | -2.56 | -2.60 | -2.68 | -2.75 | -2.65 | 0.07 |
3.3.2. Convergence properties
The cumulative reward is calculated over each training episode, and a moving average is computed over 40 episodes to generate Figure 8. Similar to the Inter-FRL experiments, Intra-FRLWA shows the most favourable training results. In addition, the rate of convergence increases with Intra-FRLWA over no-FRL and Intra-FRLGA. Lastly, the stability during training is also shown to be improved as the standard deviation across the four random seeds is much smaller than the other two cases (as evident in the shaded regions of Figure 8).
3.3.3. Test results for one episode
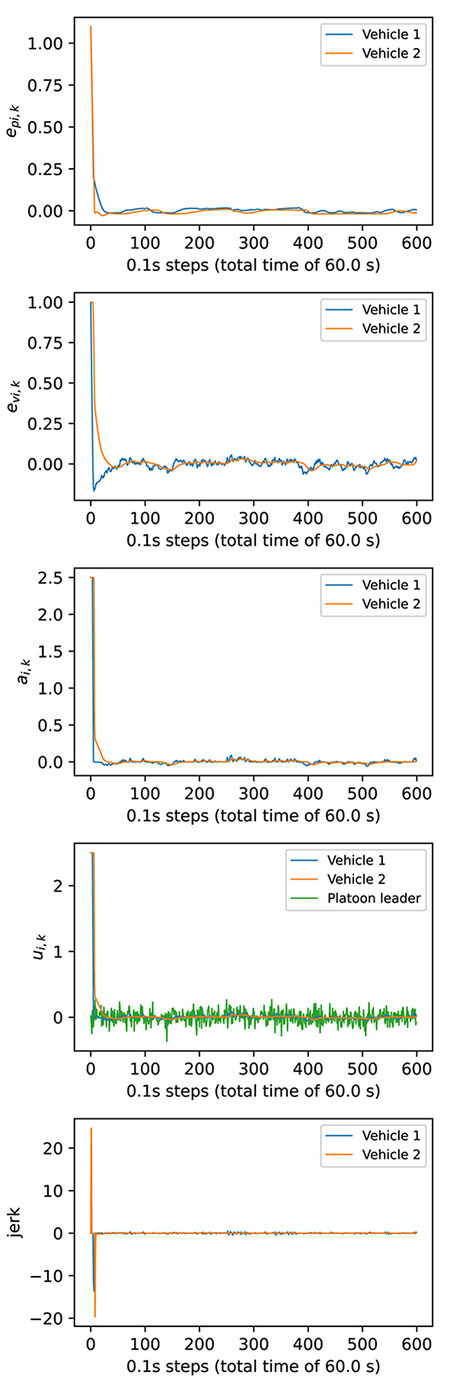
A single simulation is performed on an episode plotting the jerk, along with the control input
3.4. Comparison between inter and intra-FRL
The results for both Inter-FRL and Intra-FRL are summarized in Table 6 below.
Performance after training across 4 random seeds for both Inter and Intra FRL. Each simulation result contains 600 time steps.
| Training Method | Seed 1 | Seed 2 | Seed 3 | Seed 4 | Average system reward | Standard deviation |
| Inter-FRLGA | -2.79 | -2.81 | -3.05 | -2.76 | -2.85 | 0.11 |
| Inter-FRLWA | -2.64 | -2.88 | -2.92 | -2.93 | -2.84 | 0.12 |
| Intra-FRLGA | -2.85 | -8.05 | -4.23 | -2.99 | -4.53 | 2.10 |
| Intra-FRLWA | -2.56 | -2.60 | -2.68 | -2.75 | -2.65 | 0.07 |
It is clear that using weight aggregation in both Inter-FRL and Intra-FRL is favourable to gradient aggregation. In addition, Intra-FRLWA provides the overall best result. Intra-FRL likely converges to the best model due to conditions each agent experiences during training. For Inter-FRL, the environment is independent and identically distributed. For Intra-FRL, each follower's training depends on the policy of the preceding vehicle. For the 2 vehicle scenario studied, vehicle 1 will converge prior to vehicle 2 as vehicle 1 learns based on the stochastic random input generated by the platoon leader. As vehicle 1 is training, vehicle 2 trains based off the policy of vehicle 1. As previously stated, Inter-FRL shares parameters amongst vehicles in the same index across platoons, where-as Intra-FRL provides the advantage of sharing parameters from preceding vehicles to following vehicles. Our implementation of Intra-FRL includes a directional parameter averaging. For example, vehicle 1 does not train with averaged parameters from the followers, but vehicle 2 has the advantage of including vehicle 1's model in its averaging. This directional averaging provides an advantage to vehicle 2, as evidenced by the increased performance in Table 6.
3.5. Intra-FRL with variant number of vehicles
An additional factor to consider when evaluating FRL in relation to the no-FRL base scenario is how FRL performs with increasing agents relative to no-FRL. In this section, 12 experiments are conducted with no-FRL, and 12 with Intra-FRLWA. Each set of 12 experiments for no-FRL and Intra-FRLWA are broken up by number of vehicles and random seed. The random seed is selected to be a value between 1 and 4, inclusive. In addition, the platoons under study contain either 3, 4, or 5 vehicles. Once training has been completed for all experiments, the cumulative reward for each experiment is evaluated using a single simulation episode in which the seed is kept constant. Intra-FRLWA is used as the FRL training strategy since Intra-FRLWA was identified to be the highest performing FRL strategy in the previous section.
3.5.1. Performance with varying number of vehicles
The performance for each experiment is calculated by taking the average cumulative episodic reward across each vehicle in the platoon at the end of the simulation episode. Table 7 presents the results for no-FRL and Intra-FRLWA for platoons with 3, 4, and 5 follower vehicles. Table 7 shows that Intra-FRLWA provides favourable performance in all platoon lengths. A notable example of Intra-FRLWA's success is highlighted when considering the poor performance of the 4 vehicle platoon trained with no-FRL using seed 1. The Intra-FRLWA training strategy was able to overcome the performance challenges, correcting the poor performance entirely.
Performance after training across 4 random seeds with varying platoon lengths. Each simulation result contains 600 time steps
| Training Method | No. Vehicles | Seed 1 | Seed 2 | Seed 3 | Seed 4 | Avg. System Reward | Std. Dev. |
| No-FRL | 3 | -3.64 | -3.28 | -3.76 | -3.52 | -3.55 | 0.20 |
| No-FRL | 4 | -123.58 | -4.59 | -7.39 | -4.51 | -35.02 | 59.06 |
| No-FRL | 5 | -4.90 | -5.94 | -6.76 | -6.11 | -5.93 | 0.77 |
| Intra-FRLWA | 3 | -3.44 | -3.16 | -3.43 | -4.14 | -3.54 | 0.42 |
| Intra-FRLWA | 4 | -3.67 | -3.56 | -4.10 | -3.60 | -3.73 | 0.25 |
| Intra-FRLWA | 5 | -3.92 | -4.11 | -4.33 | -3.97 | -4.08 | 0.18 |
3.5.2. Convergence properties
The cumulative reward is calculated over each training episode, and a moving average is computed over 40 episodes to generate Figure 10. Intra-FRLWA shows favourable training performance to that of the no-FRL scenario for all platoon lengths. In addition, the rate of convergence is increased using Intra-FRLWA versus no-FRL. Furthermore, the shaded areas corresponding to standard deviation across the seeds are reduced significantly, indicating better stability across the seeds for Intra-FRLWA than no-FRL. Last, the overall stability is improved as shown by the large noise reduction during training in Figure 10d,10e,10f when compared with no-FRL's Figure 10a,10b,10c.
3.5.3. Test results for one episode
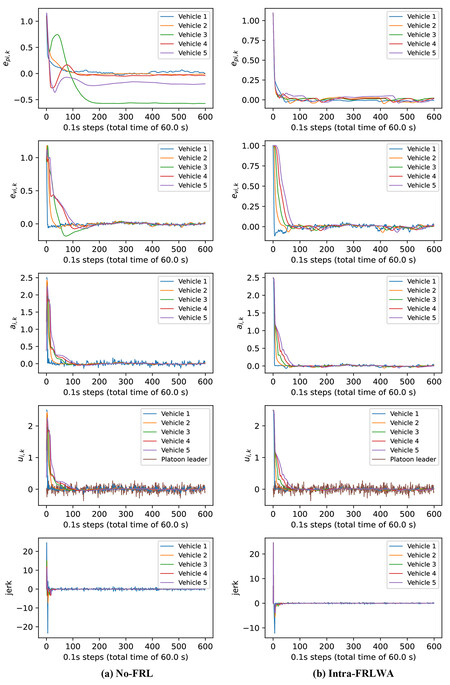
As with all previous sections, a single simulation is performed on a 60 second episode plotting the jerk along with the control input
Figure 11. Results for a specific 60s test episode using the 5 vehicle 1 platoon environment trained using no-FRL (Figure 11a), and with Intra-FRLWA (Figure 11b)
The large difference in performance for no-FRL versus Intra-FRL can be explained by understanding how Intra-FRLWA works. With no-FRL, each agent trains independently, and the inputs to the following vehicles are directly outputted from the predecessors. Thus, the followers farther back in the platoon take longer to train as their predecessors' outputs can be highly variable while training. As the policies of the predecessors converge, the policy of each follower can then begin to converge. This sequential convergence from predecessor to follower can be seen in Figure 10,where the convergence during training is slower for vehicles 4 and 5 than it is for 3, 2 and 1. Intra-FRLWA helps to resolve this challenge by allowing vehicles to average their model weights, thus distributing an aggregation of more mature predecessor parameters amongst the platoon.
4. CONCLUSION
In this paper, we have formulated an AV platooning problem and successfully applied FRL in a variety of methods to AV platooning. In addition, we proposed new approaches for applying FRL to AV platoons: Inter-FRL and Intra-FRL. By comparing FRL performance with both gradient and weight averaging in the AV platooning scenario, it has been shown that weight averaging was the optimal aggregation method regardless of using Inter-FRL or Intra-FRL. Furthermore, it was found that the Intra-FRLWA strategy was most advantageous for applying FRL to AV platooning. Finally, it was proven that applying Intra-FRLWA to AV platoons up to 5 vehicles in length provided large performance advantages during and after training when compared to AV platoons that were controlled by DDPG agents trained without FRL. These results are backed by simulations performed using models trained across four random seeds, and an additional simulation set with variable platoon sizes. The focus of this paper was on decentralized platoon control, where each follower in the platoon trains locally with respect to their individual reward.
In the future, improvements to the system could be made by implementing weighted averaging in the FRL aggregation method. Moreover, in AV platooning, communication delays can be considered in the model to give a more concrete real life example.
DECLARATIONS
Authors' contributions
Made substantial contributions to the research, idea generation, testing, and software development. Solely programmed the Python AVDDPG application for conducting the DRL experiments, simulating and aggregating experiment results. Wrote and edited the original draft: Boin C
Performed oversight and leadership responsibility for the research activity planning and execution, as well as developed ideas and evolution of overarching research aims. Assisted editing the original draft: Lei L
Performed critical review, commentary and revision, as well as provided administrative, technical, and material support: Yang S
Availability of data and materials
Not applicable.
Financial support and sponsorship
This work was supported by the Natural Sciences and Engineering Research Council (NSERC) of Canada and the CARE-AI Seed Fund at the University of Guelph.
Conflicts of interest
The authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
©The Author(s) 2022.
REFERENCES
1. McMahan HB, Moore E, Ramage D, Arcas BA. Federated learning of deep networks using model averaging. ArXiv, vol. abs/1602.05629, 2016.
2. Konecný J, McMahan HB, Ramage D. Federated optimization: Distributed optimization beyond the datacenter. ArXiv, vol. abs/1511.03575, 2015.
3. McMahan HB, Moore E, Ramage D, Hampson S, Arcas BA. Communication-efficient learning of deep networks from decentralized data. Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, AISTATS 2017, vol. 54, 2017.
4. Yang Q, Liu Y, Chen T, Tong Y. Federated machine learning: concept and Applications. arXiv, vol. 10, no. 2, pp. 1–19, 2019.
5. Lim HK, Kim JB, Heo JS, Han YH. Federated reinforcement learning for training control policies on multiple iot devices. Sensors (Basel) 2020;20: 1359. Available: https://doi.org/10.3390/s20051359.
6. Ye Y, Zhang X, Sun J. Automated vehicle's behavior decision making using deep reinforcement learning and high-fidelity simulation environment. Transportation Research Part C: Emerging Technologies 2019;107: 155-70. Available: https://doi.org/10.1016/j.trc.2019.08.011.
7. Zhu M, Wang X, Wang Y. Human-like autonomous car-following model with deep reinforcement learning. Transportation Research Part C: Emerging Technologies 2018;97: 348-68. Available: https://doi.org/10.1016/j.trc.2018.10.024.
8. Song X, Chen L, Wang K, He D. Robust time-delay feedback control of vehicular cacc systems with uncertain dynamics. Sensors (Basel) 2020;20: 1775. Available: https://doi.org/10.3390/s20061775.
9. Chu T, Kalabic U. Model-based deep reinforcement learning for CACC in mixed-autonomy vehicle platoon. Proceedings of the IEEE Conference on Decision and Control. vol. 2019-December, pp. 4079-84. [Online]. Available: https://doi.org/10.1109/CDC40024.2019.9030110.
10. Nadiger C, Kumar A, Abdelhak S. Federated reinforcement learning for fast personalization. 2019 IEEE Second International Conference on Artificial Intelligence and Knowledge Engineering (AIKE), 2019, pp. 123-127. Available: https://doi.org/10.1109/AIKE.2019.00031.
11. Qi J, Zhou Q, Lei L, Zheng K. Federated reinforcement learning: Techniques, applications, and open challenges. Intell Robot 2021;1:18-57.
12. Sutton RS, Barto AG. Reinforcement learning: An introduction. MIT press, 2018.
13. Yang Q, Liu Y, Cheng Y, Kang Y, Chen T, Yu H. Federated learning. Synthesis Lectures on Artificial Intelligence and Machine Learning 2019;13: 1-207. Available: https://doi.org/10.2200/S00960ED2V01Y201910AIM043.
14. Liu B, Wang L, Liu M. Lifelong federated reinforcement learning: a learning architecture for navigation in cloud robotic systems. arXiv, vol. 4, no. 4, pp. 4555–4562, 2019.
15. Liang X, Liu Y, Chen T, Liu M, Yang Q. Federated transfer reinforcement learning for autonomous driving. arXiv, 2019.
16. Zhang X, Peng M, Yan S, Sun Y. Deep-reinforcement-learning-based mode selection and resource allocation for cellular v2x communications. IEEE Internet of Things Journal, vol. 7, no. 7, pp. 6380–6391, 2020.
17. Lim H, Kim J, Ullah I, Heo J, Han Y. Federated reinforcement learning acceleration method for precise control of multiple devices. IEEE Access, vol. 9, pp. 76 296–76 306, 2021.
18. Wang X, Li R, Wang R, Li X, Taleb T, Leung VCM. Attention-weighted federated deep reinforcement learning for device-to-device assisted heterogeneous collaborative edge caching. IEEE Journal on Selected Areas in Communications, vol. 39, no. 1, pp. 154–169, 2021.
19. Huang H, Zeng C, Zhao Y, Min G, Zhu Y, Miao W, Hu J. Scalable orchestration of service function chains in nfv-enabled networks: A federated reinforcement learning approach. IEEE Journal on Selected Areas in Communications, vol. 39, no. 8, pp. 2558–2571, 2021.
20. Makantasis K, Kontorinaki M, Nikolos I. Deep reinforcement-learning-based driving policy for autonomous road vehicles. IET Intelligent Transport Systems 2020;14: 13-24. [Online]. Available: https://doi.org/10.1049/iet-its.2019.0249.
21. Sallab AE, Abdou M, Perot E, Yogamani S. Deep reinforcement learning framework for autonomous driving. IS and T International Symposium on Electronic Imaging Science and Technology 2017;29: 70-6. [Online]. Available: https://doi.org/10.2352/ISSN.2470-1173.2017.19.AVM-023.
22. Lin Y, McPhee J, Azad NL. Longitudinal dynamic versus kinematic models for car-following control using deep reinforcement learning. 2019 IEEE Intelligent Transportation Systems Conference (ITSC), 2019. pp. 1504–1510.
23. Peake A, McCalmon J, Raiford B, Liu T, Alqahtani S. Multi-agent reinforcement learning for cooperative adaptive cruise control. 2020 IEEE 32nd International Conference on Tools with Artificial Intelligence (ICTAI), 2020, pp. 15-22[Online]. Available: https://doi.org/10.1109/ICTAI50040.2020.00013.
24. Lillicrap TP, Hunt JJ, Pritzel A, et al. Continuous control with deep reinforcement learning. 4th International Conference on Learning Representations, ICLR 2016 - Conference Track Proceedings, 2016.
25. Lin Y, Mcphee J, Azad NL. Comparison of deep reinforcement learning and model predictive control for adaptive cruise control. IEEE Trans Intell Veh 2021;6: 221-31. Available: http://dx.doi.org/10.1109/TIV.2020.3012947.
26. Yan R, Jiang R, Jia B, Yang D, Huang J. Hybrid car-following strategy based on deep deterministic policy gradient and cooperative adaptive cruise control, 2021.
27. Zhu M, Wang Y, Hu J, Wang X, Ke R. Safe, efficient, and comfortable velocity control based on reinforcement learning for autonomous driving. CoRR, vol. abs/1902.00089, 2019. [Online]. Available: http://arxiv.org/abs/1902.00089.
28. Lei L, Liu T, Zheng K, Hanzo L. Deep reinforcement learning aided platoon control relying on V2X information. IEEE Transactions on Vehicular Technolog 2022. Available: http://dx.doi.org/10.1109/TVT.2022.3161585.
29. Lei L, Tan Y, Zheng K, Liu S, Zhang K, Shen X. Deep reinforcement learning for autonomous internet of things: Model, applications and challenges. IEEE Communications Surveys Tutorials 2020;22:1722-60.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Boin C, Lei L, Yang SX. AVDDPG – Federated reinforcement learning applied to autonomous platoon control. Intell Robot 2022;2(2):145-67. http://dx.doi.org/10.20517/ir.2022.11
AMA Style
Boin C, Lei L, Yang SX. AVDDPG – Federated reinforcement learning applied to autonomous platoon control. Intelligence & Robotics. 2022; 2(2): 145-67. http://dx.doi.org/10.20517/ir.2022.11
Chicago/Turabian Style
Boin, Christian, Lei Lei, Simon X. Yang. 2022. "AVDDPG – Federated reinforcement learning applied to autonomous platoon control" Intelligence & Robotics. 2, no.2: 145-67. http://dx.doi.org/10.20517/ir.2022.11
ACS Style
Boin, C.; Lei L.; Yang SX. AVDDPG – Federated reinforcement learning applied to autonomous platoon control. Intell. Robot. 2022, 2, 145-67. http://dx.doi.org/10.20517/ir.2022.11
About This Article
Special Issue
Copyright
Data & Comments
Data

 Cite This Article 17 clicks
Cite This Article 17 clicks
















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.