Networked scheduling for decentralized load frequency control
Abstract
This paper investigates the scheduling process for multi-area interconnected power systems under the shared but band-limited network and decentralized load frequency controllers. To cope with sub-area information and avoid node collision of large-scale power systems, round-robin and try-once-discard scheduling are used to schedule sampling data among different sub-grids. Different from existing decentralized load frequency control methods, this paper studies multi-packet transmission schemes and introduces scheduling protocols to deal with the multi-node collision. Considering the scheduling process and decentralized load frequency controllers, an impulsive power system closed-loop model is well established. Furthermore, sufficient stabilization criteria are derived to obtain decentralized ℋ∞ output feedback controller gains and scheduling protocol parameters. Under the designed decentralized output feedback controllers, the prescribed system performances are achieved. Finally, a three-area power system example is used to verify the effectiveness of the proposed scheduling method.
Keywords
1. INTRODUCTION
With the vigorous development of power markets, the degree of interconnection among power grid regions is increasing. At present, power grids have developed into multi-area interconnected power systems[1, 2]. Generally, there are two communication schemes to transmit data between neighborhood areas, that is, the dedicated channel and the open infrastructure. Since the latter has outstanding advantages over the former, such as higher flexibility and lower cost, it has been widely used in the communication of multi-area interconnected power systems[3-5].
An important indicator to measure power system operation quality is the fluctuation in frequency, and load frequency control (LFC) is widely used to maintain frequency interchanges at scheduled values and stifle frequency fluctuation caused by load disturbances[2, 6, 7]. Under the open communication infrastructure, the sensor in each area collects data information. Then, data is transmitted to the decentralized controller under the shared but band-limited network. The corresponding control commands are issued to actuators in each area respectively. However, due to the introduction of the network, the design and operation of LFC face some new challenges, such as node collision, data loss and network-induced delay[8-10].
Due to different locations of sub-region power grids and the wide distribution of system components, multi-channel transmission is inevitable in multi-area interconnected power systems, while most of the existing results[10-13] take the general assumption that sampled data is packaged into a single packet to transmit, which is not applied in large-scale multi-area interconnected power systems. On the other hand, the shared network has limited bandwidth, where the simultaneous transmission under multiple channels may cause node congestion. To solve this problem, scheduling protocols have been presented to decide which node to gain access to the communication network[14, 15].
Generally, multi-channel scheduling includes Round-Robin (RR) scheduling[16, 17], try-once-discard (TOD) scheduling[18, 19], and stochastic scheduling[20]. Under the RR scheduling protocol, each node is transmitted periodically with a fixed period whose value is the total number of transmission channels. Under the TOD scheduling, the sensor node with the largest scheduling error has access to the channel. Recently, a time-delay analysis method has been discussed to derive stability criteria for networked control systems (NCSs) which are scheduled by the above three communication protocols[14, 21]. Besides, a hybrid system method has been employed to analyze NCSs with variable delays under the TOD communication protocol[19], where a partial exponential stabilization criterion has been derived. The
This paper studies the
(1) RR and TOD protocols are used to deal with the multi-node collision of large-scale power systems, which improve communication efficiency greatly. Compared with the existing LFC methods[10, 23, 24], the scheduling process under multi-area transmission schemes is investigated.
(2) An networked power system impulsive closed-loop model is well constructed, which covers the multi-channel scheduling, packet dropout, disturbance, and network-induced delays in a unified framework. Compared with the system without disturbance[19], this paper studies the anti-disturbance performance of the studied system. An
1.1. Notations
Throughout this paper,
2. PROBLEM FORMULATION
Considering single-packet size constraints, the dynamic model of multi-area interconnected power systems with decentralized load frequency controllers is constructed in this section. An impulsive system model under TOD or RR protocol is established.
2.1. Multi-area decentralized LFC model
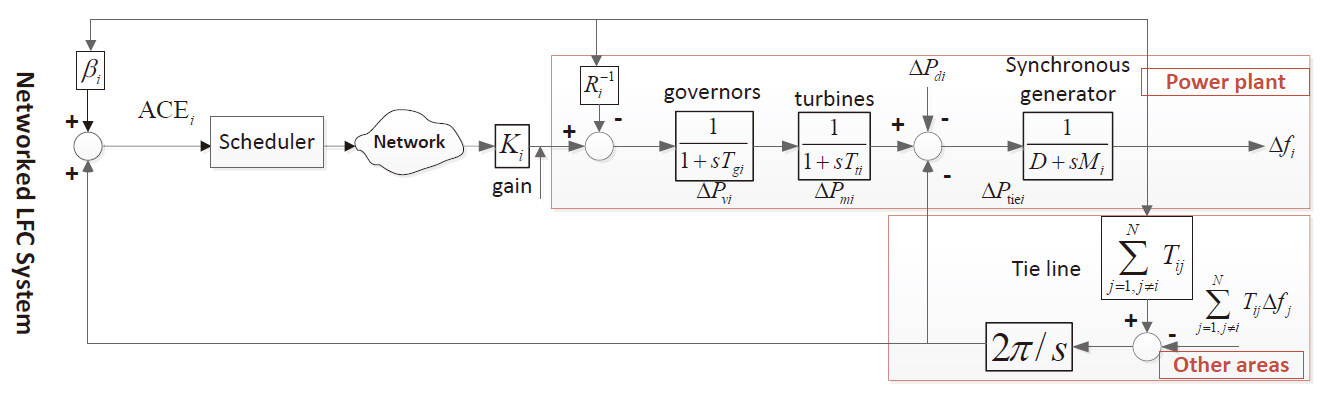
Diagram of the multi-area decentralized LFC under scheduling protocols is shown in Figure 1, where data transmission from sensors to decentralize controllers is scheduled by RR or TOD scheduling protocol.
The system model is represented as[23, 25]:
where
The state and measured output signals are
where
The multi-area power system includes
In this paper, we take imperfect network conditions into account, such as data loss and network-induced delay. Denote the sequence after packet loss by
Let
Consider the scheduling error between output
where
Under RR scheduling protocol, the active node
In the following, we will design the decentralized LFC law under the communication network. Similar to[23], a PI controller is used in this paper:
Therefore, dynamic model of the scheduled power systems under the decentralized LFC Equation (8) and imperfect network environments can be formalized as
where
2.2. Impulsive model and study objective
From Equation (5), one can obtain that
Define an artificial delay
From Equation (5) and Equation (9), the impulsive power system model can be
For system Equation (12), the initial condition of
Using scheduling scheme Equation (6) and Equation (7), this paper is to design the decentralized controller Equation (8) such that system Equation (12) is exponentially stable with a prescribed
3. MAIN RESULTS
In the following, we first derive sufficient criteria under scheduling scheme Equation (6) and Equation (7) to ensure the exponential stability of system Equation (12) with a prescribed
3.1. Stability analysis under the TOD scheduling scheme Equation (6)
Construct Lyapunov-Krasovskii functional candidate:
where
Remark 1
Theorem 1Under TOD scheduling scheme Equation (6), for given scalars
are feasible for
Proof: Differentiating
where
We use the reciprocally convex approach[27] to deal with the cross item in Equation (18). By using Schur's complement, one can get
In the following, we will prove that
(ⅰ) with
Since
It follows from
where
Then taking Equation (17) and Equation (22) into account, denoting
Hence, one can conclude that
From Equation (24), we have
which implies that
It follows from
For
Clearly, there exists the maximum of
Therefore, the exponential stability of the system Equation (12) with
Next, we will show that
(ⅱ) under the zero initial condition, the inequality
From Equation (19), we obtain that for
Integrating Equation (27) on
Then, by summing Equation (28) on
Under the zero initial condition,
Remark 2The feasibility of the linear martix inequalities has been sufficiently explained in[23, 28]. Due to page limitations, this part is omitted here.
3.2. Stability analysis under the RR scheduling scheme Equation (7)
Construct the following Lyapunov-Krasovskii functional candidate:
where
Similar to Theorem 5.2 in[29], we establish the following result.
Theorem 2Under RR scheduling scheme Equation (7), given
Proof: The detailed derivation process can refer to[29] and the proof of Theorem 1, which is omitted here due to the limited pages.
3.3. Controller Design under the TOD scheduling scheme Equation (6)
Theorem 3.3.Under TOD scheduling scheme Equation (6), for given matrices
is solvable, and the controller gain is given by
Proof: Let
and their transposes, respectively. For the nonlinear terms
3.4. Controller design under the RR scheduling scheme Equation (7)
Similar to Theorem 5.2 in[29], we establish Theorem 4.
Theorem 4Under the RR scheduling scheme Equation (7), for given matrices
Proof: The detailed derivation process can refer to[29] and the proof of Theorem 3, which is omitted here.
4. AN ILLUSTRATIVE EXAMPLE
In the following, we use a three-area power system[23, 24, 28] interconnected by the shared communication network to demonstrate the effectiveness of main results. Parameters are listed in Table 1.
Configuration of three-area power systems
| 0.30 | 0.37 | 0.05 | 1.0 | 10 | ||
| 0.17 | 0.40 | 0.05 | 1.5 | 10 | ||
| 0.20 | 0.35 | 0.05 | 1.8 | 12 | ||
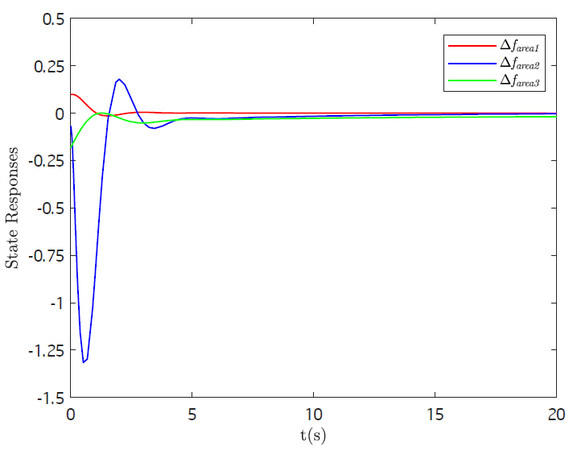
Case 1: Stability of the studied system under TOD scheduling scheme Equation (6) and
Assume parameters are chosen as
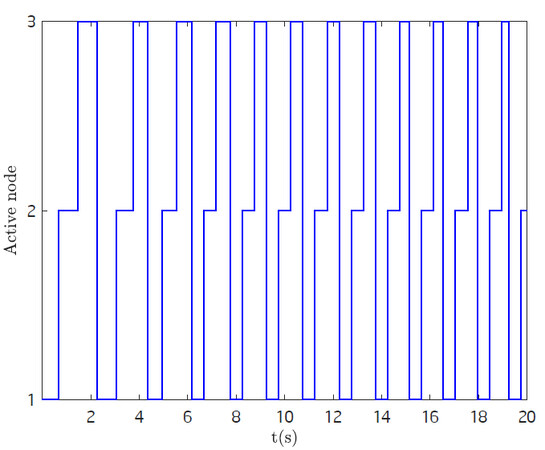
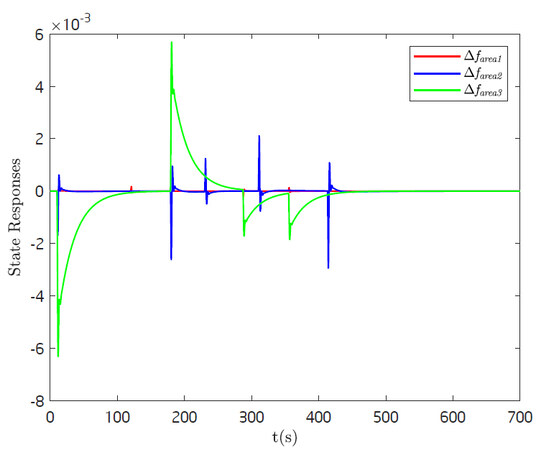
Correspondingly, state responses and the switching behavior of active nodes are illustrated by Figure 2 and 3, respectively. Clearly, the designed dynamics output feedback controllers can stabilize the three-area power system under the TOD scheduling scheme Equation (6) in the absence of disturbance.
Case 2: Stability of the studied system under RR scheduling scheme Equation (7) and
To compare with the TOD protocol Equation (6), we use the same parameters as case 1. We apply Theorem 4 which yields
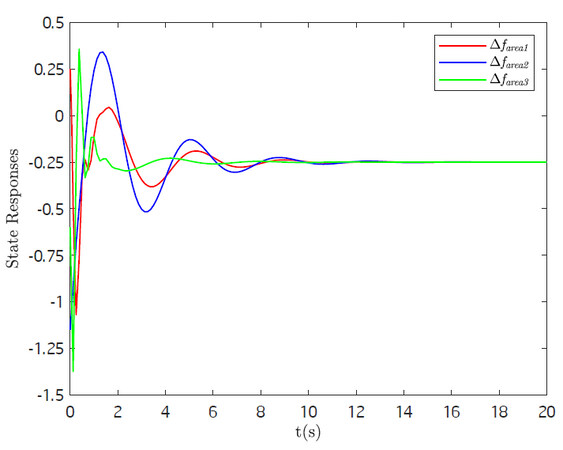
Case 3: Stability of the studied system under TOD scheduling scheme Equation (6) and
According to Theorem 1-4, TOD protocol can degrade into RR protocol under certain conditions. In this case, we take the TOD protocol Equation (6) as an example to verify the anti-disturbance performance of the studied system. Under the disturbance
5. CONCLUSIONS
This paper has designed
DECLARATIONS
Authors' contributions
Made substantial contributions to the research, idea generation, algorithm design, performed critical review, commentary and revision, as well as provided administrative, technical, and material support: Peng C
Conceived and designed the experiments, analyzed simulation results, wrote and edited the original draft: Yang H
Financial support and sponsorship
This work was supported in part by the National Natural Science Foundation of China under Grant 62173218, and the International Corporation Project of Shanghai Science and Technology Commission under Grant 21190780300.
Availability of data and materials
Not applicable.
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2022.
REFERENCES
1. Mohandes B, El Moursi MS, Hatziargyriou N, El Khatib S. A review of power system flexibility with high penetration of renewables. IEEE Trans Power Syst 2019;34:3140-55.
2. Ranjan M, Shankar R. A literature survey on load frequency control considering renewable energy integration in power system: Recent trends and future prospects. J Energy Stor 2022;45:103717.
3. Peng C, Li F. A survey on recent advances in event-triggered communication and control. Inform Sci 2018;457:113-25.
4. Zhou Q, Shahidehpour M, Paaso A, et al. Distributed control and communication strategies in networked microgrids. IEEE Communic Surv & Tutori 2020;22:2586-633.
5. Shang Y. Group consensus of multi-agent systems in directed networks with noises and time delays. Int J Syst Sci 2015;46:2481-92.
6. Alhelou HH, Hamedani-Golshan ME, Zamani R, Heydarian-Forushani E, Siano P. Challenges and opportunities of load frequency control in conventional, modern and future smart power systems: a comprehensive review. Energies 2018;11:2497.
7. Yan Z, Xu Y. Data-driven load frequency control for stochastic power systems: a deep reinforcement learning method with continuous action search. IEEE Trans Power Syst 2018;34:1653-56.
8. Peng C, Wu J, Tian E. Stochastic event-triggered
9. Shangguan XC, He Y, Zhang CK, et al. Control performance standards-oriented event-triggered load frequency control for power systems under limited communication bandwidth. IEEE Trans Contr Syst Technol 2021;30:860-68.
10. Tian E, Peng C. Memory-based event-triggering
11. Peng C, Sun H, Yang M, Wang YL. A survey on security communication and control for smart grids under malicious cyber attacks. IEEE Trans Syst, Man, Cybern: Systems 2019;49:1554-69.
12. Wang D, Chen F, Meng B, Hu X, Wang J. Event-based secure
13. Wu J, Peng C, Yang H, Wang YL. Recent advances in event-triggered security control of networked systems: a survey. Int J Syst Sci 2022;0:1-20.
14. Freirich D, Fridman E. Decentralized networked control of systems with local networks: a time-delay approach. Automatica 2016;69:201-9.
15. Liu K, Fridman E, Hetel L, Richard JP. Sampled-data stabilization via round-robin scheduling: a direct Lyapunov-Krasovskii approach. IFAC Proceed Vol 2011;44:1459-64.
16. Ding D, Wang Z, Han QL, Wei G. Neural-network-based output-feedback control under round-robin scheduling protocols. IEEE trans cybern 2018;49:2372-84.
17. Zou L, Wang Z, Han QL, Zhou D. Full information estimation for time-varying systems subject to Round-Robin scheduling: A recursive filter approach. IEEE Trans Syst, Man, Cybern: Systems 2019;51:1904-16.
18. Zhang XM, Han QL, Ge X, et al. Networked control systems: a survey of trends and techniques. IEEE/CAA J Autom Sinica 2019;7:1-17.
19. Liu K, Fridman E, Hetel L. Network-based control via a novel analysis of hybrid systems with time-varying delays. In: 2012 IEEE 51st IEEE Confer Decis Contr (CDC). IEEE; 2012. pp. 3886-91.
20. Zhang J, Peng C, Xie X, Yue D. Output feedback stabilization of networked control systems under a stochastic scheduling protocol. IEEE trans cybern 2019;50:2851-60.
21. Liu K, Fridman E, Johansson KH. Networked control with stochastic scheduling. IEEE Trans Autom Contr 2015;60:3071-76.
22. Zhang J, Peng C. Networked
23. Peng C, Zhang J, Yan H. Adaptive event-triggering
24. Sun H, Peng C, Yue D, Wang YL, Zhang T. Resilient load frequency control of cyber-physical power systems under QoS-dependent event-triggered communication. IEEE Trans Syst, Man, Cybernet: Systems 2020;51:2113-22.
25. Shang Y. Median-based resilient consensus over time-varying random networks. IEEE Trans Circ Syst Ⅱ: Express Briefs 2021;69:1203-7.
26. Seuret A, Gouaisbaut F. Wirtinger-based integral inequality: application to time-delay systems. Automatica 2013;49:2860-66.
27. El Ghaoui L, Oustry F, AitRami M. A cone complementarity linearization algorithm for static output-feedback and related problems. IEEE trans autom contr 1997;42:1171-76.
28. Peng C, Li J, Fei M. Resilient Event-Triggering
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Peng C, Yang H. Networked scheduling for decentralized load frequency control. Intell Robot 2022;2(3):298-312. http://dx.doi.org/10.20517/ir.2022.27
AMA Style
Peng C, Yang H. Networked scheduling for decentralized load frequency control. Intelligence & Robotics. 2022; 2(3): 298-312. http://dx.doi.org/10.20517/ir.2022.27
Chicago/Turabian Style
Peng, Chen, Hongchenyu Yang. 2022. "Networked scheduling for decentralized load frequency control" Intelligence & Robotics. 2, no.3: 298-312. http://dx.doi.org/10.20517/ir.2022.27
ACS Style
Peng, C.; Yang H. Networked scheduling for decentralized load frequency control. Intell. Robot. 2022, 2, 298-312. http://dx.doi.org/10.20517/ir.2022.27
About This Article
Copyright
Data & Comments
Data

 Cite This Article 13 clicks
Cite This Article 13 clicks














Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.