T-S fuzzy-model-based adaptive cruise control for longitudinal car-following considering vehicle lateral stability
Abstract
Adaptive cruise control is one of the essential technologies of advanced driver assistance systems, which is used to maintain a safe distance between an ego vehicle and a preceding vehicle and has been extensively applied in the automotive industry and control community. Note that some vehicle manoeuvres may approach handling limits to prevent collisions under complex road conditions, which often leads to vehicle lateral instability while cruising. In this study, a T-S fuzzy model predictive control framework is applied to the problem of adaptive cruise control. Variations in the preceding vehicle velocity and road surface conditions are considered to formulate adaptive cruise control as a tracking control problem of a T-S fuzzy system subject to parameter uncertainties and external persistent perturbations. Then, a robust positively invariant set is introduced to derive an admissible T-S fuzzy controller by solving a min-max optimization problem under a series of linear matrix inequality constraints. Finally, a CarSim/MATLAB joint simulation is conducted to illustrate the effectiveness of the proposed method, which ensures longitudinal adaptive cruise control for a car-following scenario with lateral vehicle stability.
Keywords
1. INTRODUCTION
Advanced driver assistance systems (ADASs) play a critical role in the automobile industry [1] by significantly decreasing drivers' workload while considerably improving driving safety and comfort [2–5]. A few examples of common applications of ADASs in automobiles in recent years are lane-keeping assist (LKA), adaptive cruise control (ACC), electronic stability control (ESC), and the precrash system (PCS)[6]. The ACC system is one of the first ADAS technologies for maintaining a safe distance between an ego car and a preceding vehicle[7]. Radar sensors detect the velocity of the preceding vehicle, which the ACC system uses to automatically modify the speed of the driving vehicle by managing the throttle opening or brake pedal levels[8].
Many adaptive cruise control strategies can be found in the literature to achieve longitudinal car-following and enhance driving performance. A fuzzy logic control technique is described in Ref.[9] that executes the ACC function on an AIT intelligent vehicle using the distance error and relative velocity information. In Ref.[10], a control system is presented that decreases vehicle waiting time at stop lights, as well as fuel consumption, by utilizing upcoming traffic signal information and short-range radar for optimal velocity trajectory planning. In Ref.[11], a safe and comfortable longitudinal automation system with a human-in-the-loop strategy is integrated into an ACC system. In Ref.[12], the use of a longitudinal controller for a smart and green ACC system is investigated to minimize energy expenditure and maximize energy regeneration.
Model predictive control (MPC) is a traditional control approach with demonstrated utility for solving multiobjective optimization problems under a variety of system constraints[13, 14]. In the past few years, MPC has been widely applied to the design of ACC systems. A few examples are presented here: in Ref.[15], MPC is applied to the design of spacing-control laws for transitional vehicle manoeuvres. A fuel economy-oriented ACC system is developed in Ref.[16] to minimize vehicle fuel consumption, and a generic scale reduction framework is formulated to alleviate computational loads induced by the MPC optimization solution. In Ref.[17], a benchmark setting for the MPC on a piecewise affine system is presented for the design of ACC algorithms, and different methods are implemented and evaluated to assess their main attributes, characteristics, and strong/weak points. A stochastic MPC approach for minimizing vehicle fuel consumption is investigated in Ref.[18]. An MPC method for increasing vehicle tracking accuracy and reducing fuel consumption is developed [19] by taking into account external road information, spatiotemporal constraints and nonlinear powertrain dynamics. In Ref.[20], a personalized ACC system based on driving style identification is proposed to accommodate various driving types within an MPC framework.
The Takagi-Sugeno (T-S) fuzzy system consists of a cluster of linear subsystems as an approximation for a nonlinear system. Extensive studies have been performed on this system in recent decades[21–24]. In vehicle control, vehicle dynamics are typically regarded as linear parameter varying (LPV) systems because of inevitable variations in parameters, such as longitudinal and lateral velocities. T-S fuzzy systems are constructed to model the vehicle dynamics and address parameter variations in the system. For example, in Ref.[25], a fuzzy path-tracking controller is designed considering uncertain lateral tire forces, a time-varying vehicle speed, steering-input saturation and vehicle state conditions. In Ref.[26], a fuzzy-model-based
The aforementioned literature review shows that substantial progress has been made in both theoretical formulations and practical applications of ACC design for car-following within the model-based predictive control framework. Notably, cars may lose lateral stability when employing a cruise controller in some emergency situations, such as rapid braking on roads with low friction coefficients. Thus, vehicle lateral stability needs to be considered when developing ACC strategies. In some studies, a linear force relationship is utilized between tires and roads, which does not precisely describe the lateral dynamical characteristics involved, leading to severe degradation or even instability of a closed-loop system, especially when a vehicle travels at high acceleration. The longitudinal velocity is intrinsically time-varying but is regarded as a constant in a few studies, which should also be addressed. The present study has been motivated by all these considerations.
The problem of adaptive cruise control design for longitudinal car-following considering vehicle lateral stability is investigated in this study. Vehicle longitudinal car-following kinematics are used in conjunction with two degrees-of-freedom vehicle lateral dynamics to formulate an adaptive cruise control system as a robust tracking control problem of a T-S fuzzy system by considering real-time variations of the velocity of the preceding vehicle. The corresponding control problem is then transformed into a min-max optimization problem within the T-S fuzzy control framework. The concept of robust positively invariant sets is introduced to effectively address some external norm-bounded disturbances, such as the steering angle of the front wheel and the acceleration of the preceding vehicle, to ensure that the states of the closed-loop tracking dynamics converge to a compact set. Finally, results of simulations using the CarSim/MATLAB joint platform are presented to demonstrate the effectiveness of using the proposed adaptive cruise controller to realize longitudinal car-following while ensuring vehicle lateral stability.
The main contributions of this study are as follows:
(1) a T-S fuzzy control framework is used to first establish a unified T-S fuzzy dynamical model for car-following based on a combination of longitudinal kinematics, lateral dynamics, time-varying vehicle velocity, and nonlinear lateral tire/road forces as a basis for designing adaptive cruise control;
(2) a method is proposed for designing a coordinated controller of an adaptive cruise control system and a direct yaw moment control system that ensures simultaneous vehicle longitudinal car-following and lateral stability;
(3) the developed controller design method is validated by tests in a high-fidelity CarSim/Simulink joint simulation environment, and the results clearly show the effectiveness of the T-S fuzzy model predictive controller and its superiority over a conventional controller design process that does not consider vehicle lateral stabilization.
The remainder of this paper is organized as follows. A mathematical model for a vehicle is presented in Section II, which includes longitudinal kinematics, lateral dynamics, and a tire/road force model. A design for a robust T-S fuzzy model predictive controller is presented in Section III. In Section IV, the lower layer of the designed adaptive cruise control algorithm is described. The CarSim/Simulink joint simulation results are presented in Section V. Finally, we conclude the paper in Section VI.
Notations and definitions: The notations used throughout this paper are quite standard. For any
2. METHODS
2.1. Vehicle longitudinal kinematic model
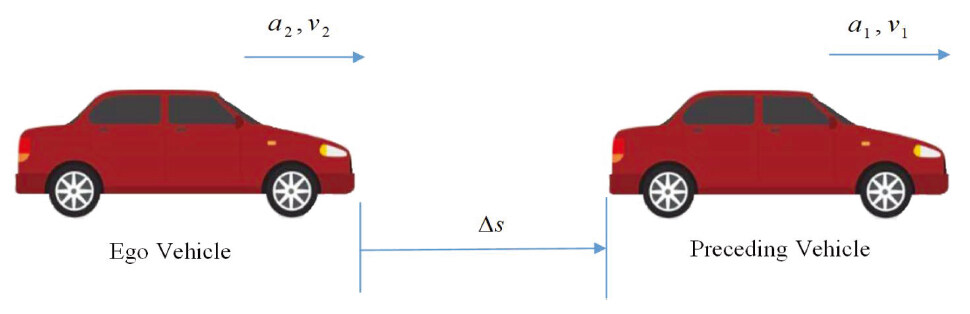
The following symbols are used in the car-following situation shown in Figure 1:
The desired spacing distance between the preceding and ego vehicles is given as follows [28]:
where
The difference in the desired and actual distances between the vehicles is defined as
Considering the time delay of the engine in the driving system, we employ a first-order system to relate the actual vehicle longitudinal acceleration
where
The definitions given above are used to express the vehicle longitudinal kinematic model as follows:
2.2. Vehicle lateral dynamics
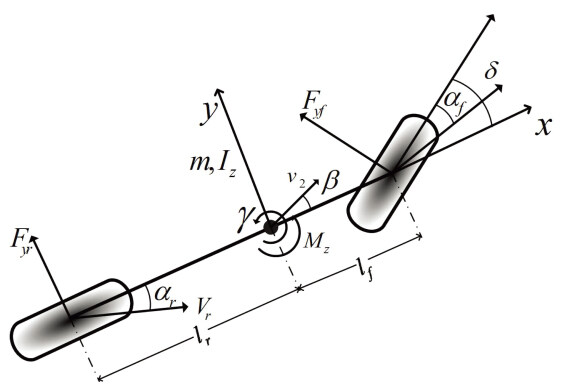
Figure 2 shows the classical two-degree-of-freedom (2-DOF) bicycle model of vehicle dynamics, which is simplified in this study by collapsing each axle to a single tire to reflect the fundamental features of lateral motions.
The mass of the ego vehicle is
where
2.3. Tire/road force model
The vehicle lateral tire/road force is generated by contact between the vehicle tires and the road surface[30]. A tire operates in the linear region for a small vehicle lateral acceleration, which can be characterized by the cornering stiffness of the front and rear tires
where
However, at high lateral acceleration, the tire/road force may not be linearly proportional to the slip angle owing to differences in the road surface characteristics and cannot be simply expressed in terms of a constant cornering stiffness and sideslip angles. Therefore, we adopt an uncertain cornering stiffness, which varies over a range, to model the uncertainty in the tire/road force [31]:
where
2.4. Vehicle-following system with lateral stability
Longitudinal kinematics, lateral dynamics, and an uncertain tire/road force model are integrated to formulate the following model for closed-loop car-following dynamics [32]:
where
The uncertain terms
and
Note that in the car-following scenario, the velocity of the ego vehicle varies with that of the preceding vehicle to maintain a desired safe distance. In this study, we assume that the velocity of the preceding car varies within a bounded range
2.5. T-S fuzzy modeling for longitudinal car-following with vehicle lateral stability
For real-time implementation of the proposed T-S fuzzy model predictive controller in the discrete-time domain, we adopt Euler's discretization method with the sampling time
where
As the velocity of the ego vehicle
The T-S fuzzy modelling approach is then employed to describe the time-varying car-following dynamics. We use the classical sector nonlinearity method to derive the discrete-time T-S fuzzy model given in Equation (9):
Fuzzy rule
where
where
where
Note that using the sector nonlinearity modelling approach with the premise variables
where
The new premise variable
where
The number of subsystems in the T-S fuzzy model Equation (10) is thus reduced from
3. T-S FUZZY MODEL PREDICATIVE CONTROL DESIGN
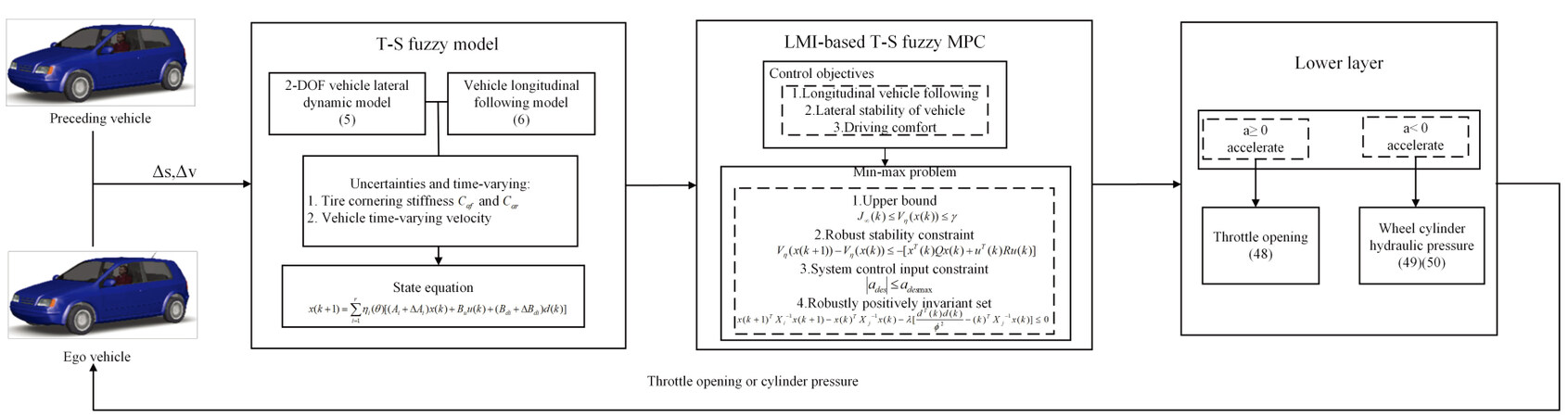
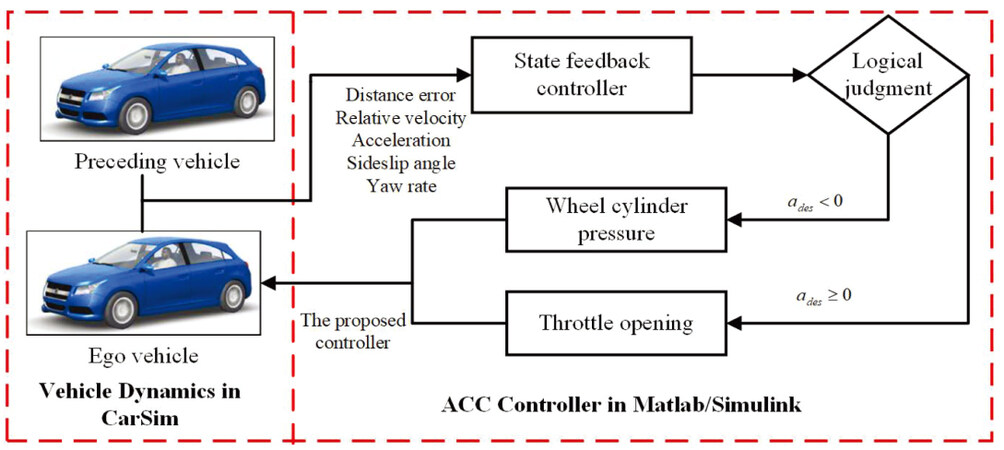
In this section, we provide a detailed description of the design of an adaptive cruise controller with lateral stability based on the T-S fuzzy MPC framework. Figure 3 shows the proposed adaptive cruise control system divided into upper and lower layers. The upper layer calculates the required acceleration and direct yaw moment for vehicle-following control subject to various constraints, and the lower layer calculates the vehicle throttle opening or hydraulic cylinder pressure of the four wheels to generate control signals corresponding to the results provided by the upper layer. Before proceeding further, some definitions and lemmas are first stated.
3.1. Robust positively invariant set
Consider a discrete-time dynamical system
where
Definition 3.1: If
Lemma 3.1[34]: The following two expressions are equivalent for System [Equation (18)] with
● the ellipsoidal set
● the inequality
3.2. Input-to-state stability
We define input-to-state stability (ISS) for use in the following sections.
Definition 3.2: A discrete-time system
where
Definition 3.3: A function
Lemma 3.2[35]: A system is said to have ISS if it admits a continuous ISS-Lyapunov function.
3.3. T-S fuzzy model-based predictive control
We adopt the following model within the framework of predictive control to represent the future dynamics of the T-S fuzzy system for vehicle-following considering lateral stability:
where
where
Consider the following objective function
where
As the cost function cannot be optimized in real time due to the unknown external disturbance, the upper limit of the cost function is minimized here. We define the following fuzzy quadratic Lyapunov function:
where
Add both sides of the inequality from
which implies that we can infer the upper bound of the objective function
Defining
Then, the aforementioned optimization problem is converted into the minimization of the upper bound of the infinite-horizon objective function:
A state feedback law
which is equivalent to
holds.
Here, we introduce a lemma for use in the following sections.
Lemma 3.3[37]: For matrices
holds for all
By Lemma
where
We also need to consider the control input constraints to ensure driving comfort:
According to inequality [Equation (26)], we have:
Therefore, we have:
Considering the Schur complement, the input constraint can be guaranteed by the following LMI if there exists a symmetric matrix
where
To deal with the external disturbance, the concept of RPI is introduced to ensure the closed-loop stability of car-following system. According to the concept of RPI and quadratic boundedness as shown in Lemma
holds under
where
The S-procedure is used to obtain a sufficient condition as follows:
where
By Lemma
Therefore, the controller design can be summarized as the following:
The T-S fuzzy state feedback controller is derived by solving the optimization problem in Equation (40) under parameter uncertainties and external persistent perturbations. The inequality Equation (34) ensures that the cost function
Remark 3.1: Note that
Theorem 3.1: The optimization problem Equation (40) has the property of recursive feasibility, that is, a solution will always exist once the problem is initially solvable.
Proof: Implementation of the predictive control strategy based on the T-S fuzzy model requires the constrained optimization problem Equation (40) to be solved at each time instant. Therefore, it is important to guarantee the recursive feasibility of the optimization problem. As an external disturbance is considered, the recursive feasibility is no longer a natural characteristic of the proposed controller. In this study, only the constraint Equation (26) depends on the time instant
Note that the inequality Equation (26) is equal to
Theorem 3.2: The closed-loop system in this paper has ISS based on the proposed MPC strategy under an external disturbance.
Proof: It has been proven that the optimization problem Equation (41), once solvable, will always be solvable.
Define the optimal solution at time instant
Furthermore, from inequality Equation (24), we can derive the following inequality:
where
From the inequalities Equation (42), Equation (44) and Lemma
4. LOWER LAYER
According to the vehicle longitudinal motions in the car-following scenario, the lower layer is divided into two blocks for calculating the acceleration throttle opening and the brake pressure, which are designed to realize the desired longitudinal acceleration or deceleration and direct yaw moment. To this end, a logic switch in the lower layer is utilized to implement an accelerating or braking manoeuvre based on the desired longitudinal acceleration
4.1. Accelerating control
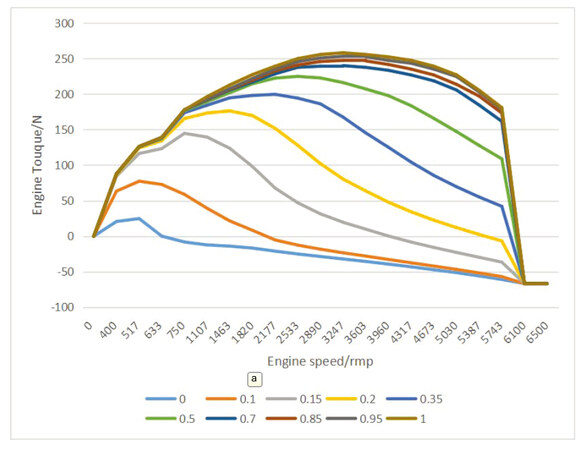
Figure 4 shows the engine speed versus the torque at different throttle openings, which are shown at the bottom. If the engine speed
The vehicle longitudinal dynamics are produced by the combined effect of vehicle traction, wind resistance, and ground resistance. Therefore, the vehicle state depends strongly on the road smoothness and the magnitude of the wind resistance coefficient during cruising. The equivalent air friction during longitudinal driving is
where
During vehicle acceleration, the engine torque
where
Then,
Thus, the corresponding expected throttle opening
4.2. Braking control
During vehicle braking, the desired acceleration
where
Equation (50) can be solved for the longitudinal force on the four wheels. Then, we can calculate the hydraulic pressure wheel cylinder from the following equation:
where
5. SIMULATION VALIDATIONS
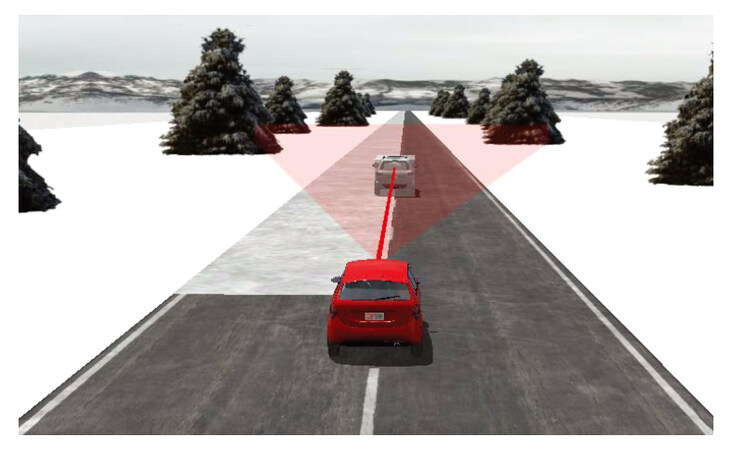
CarSim/Simulink joint simulations are conducted to verify the effectiveness of the proposed predictive control based on the T-S fuzzy model. The structure of the car-following system is shown inFigure 5. The proposed controller is derived by solving the optimization problem in Equation (41) with the YALMIP toolbox introduced in [41] within the MATLAB/Simulink environment, where the vehicle model and road conditions are provided by the CarSim platform. We simulate a severe riding condition by considering a road with snow cover on the left-hand side of the vehicle. The test scenario is shown in Figure 6.
The B-Class Hatchback car is selected as the ego vehicle to be controlled, and its physical parameters are given in Table 1. We illustrate the advantages of the methods developed in this study by comparison against a conventional controller design without vehicle lateral stabilization.
Parameters in the simulation model
| Parameters | Values |
| 1110 | |
| 1343.1 | |
| 0.25 | |
| 1480 | |
| 350 | |
| 298 | |
| 2 | |
| 66900 | |
| 62700 |
The preceding vehicle is set to be
5.1. Case I: ramp speed profile
The initial condition in this case is a zero relative velocity between vehicles: we assume
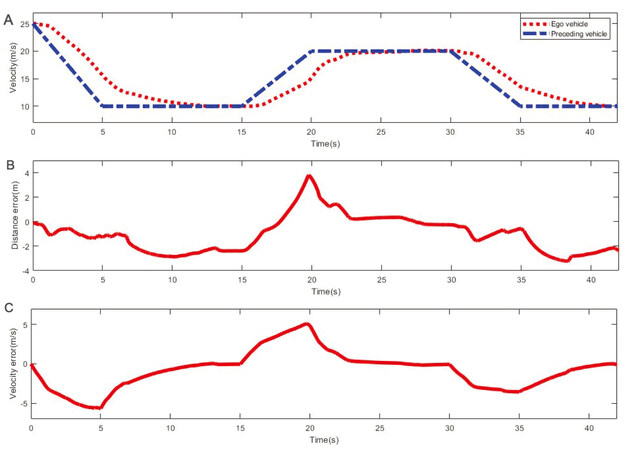
The optimization problem given by Equation (41) is solved recursively to yield the closed-loop system responses in the CarSim/Simulink joint simulation environment, which are shown in Figure 7. In Figure 7A, the blue and red curves represent the speeds of the preceding and ego vehicles, respectively. Figure 7B and Figure 7C show the errors in the longitudinal velocity and between the desired and actual longitudinal distances, respectively, where the maximum velocity error is 5.9 m/s at 4.5 s and the maximum distance error is 3.8 m at 19.7 s. Figure 7 shows that although the preceding vehicle velocities vary in the range
Figure 7. (A) Velocity of the preceding and ego vehicle; (B) Relative velocity; (C) Relative distance.
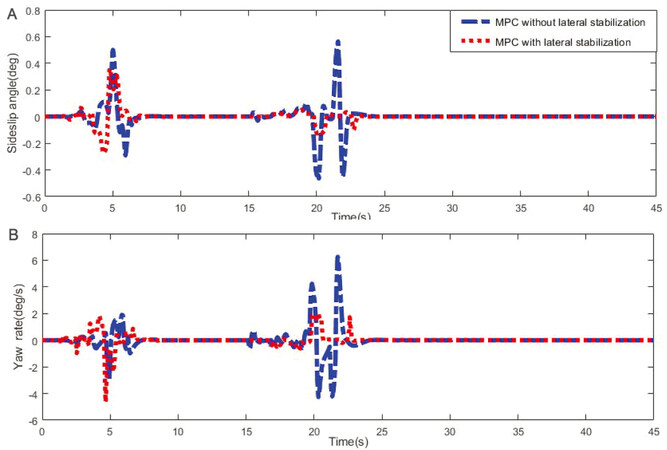
To further demonstrate the advantages of the proposed car-following controller design, Figure 8 shows the responses of sideslip angles and yaw rate (which reflect the lateral stability of the vehicle) obtained using the conventional controller (without consideration of the lateral stability) and the controller developed in this study. Figure 8 shows that compared to the results obtained using the conventional controller, the sideslip angle and yaw rate obtained using the proposed controller are smaller in magnitude, indicating improved vehicle stability.
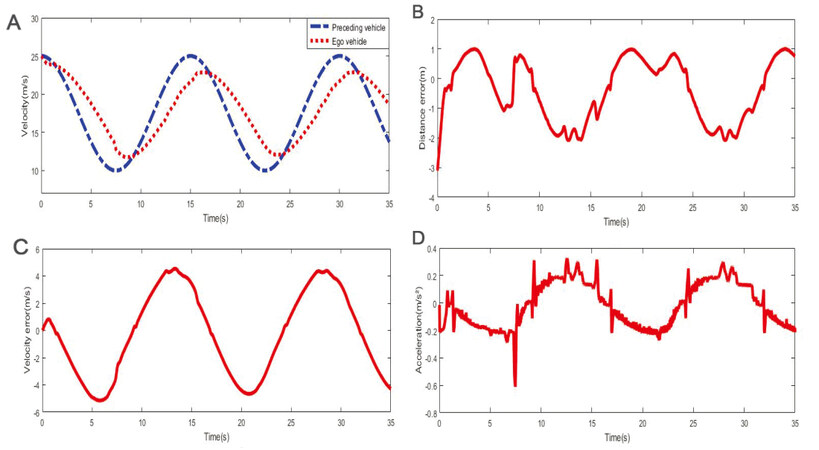
5.2. Case II: $$ cosine $$
In this case, the initial velocities of the preceding and ego vehicles and the relative distance are set to 25 m/s and 50 m, respectively. Figure 9A shows the
Figure 9. (A) Velocity of preceding and ego vehicle; (B)Relative velocity; (C) Relative distance; (D)Ego vehicle acceleration.
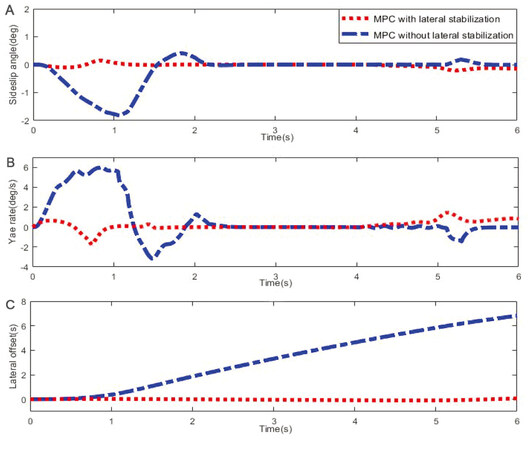
It can be concluded from Figure 9 that the proposed method completes the car-following task with satisfactory performance for a time-varying velocity. Figure 10 shows the dynamics of the sideslip angle, yaw rate, and vehicle lateral offset. Figure 10C clearly shows that the lateral offset increases when the car-following manoeuvre is conducted under the conventional MPC without lateral stabilization. These three aspects of the results show that the proposed car-following controller outperforms the conventional controller in terms of guaranteeing both satisfactory tracking performance and lateral stability of the vehicle in emergency scenarios.
6. CONCLUSION
In this paper, a T-S fuzzy model-based predictive adaptive cruise controller is designed while ensuring vehicle lateral stability by integrating the ACC system with a direct yaw moment control system. To consider variations in the preceding vehicle velocity and road surface conditions, the adaptive cruise control is formulated as a tracking control problem of a T-S fuzzy system subject to parameter uncertainties and external persistent perturbations. Then, a robust positively invariant set is introduced to develop an admissible T-S fuzzy controller by solving a min-max optimization problem under a series of linear matrix inequality constraints. CarSim/Simulink joint simulation results verify that the developed method exhibits good performance for vehicle tracking and ensures vehicle lateral stability.
DECLARATIONS
Authors' contributions
Made substantial contributions to conception and design of the study and performed data analysis and interpretation: Zhang C, Wei X
Performed data acquisition, as well as provided administrative, technical, and material support: Wang Z, Zhang H, Guo X
Availability of data and materials
In this paper, we have detailed a modelling procedure and the construction of an optimization problem with linear matrix inequality constraints to design a T-S fuzzy model predictive controller. The physical parameters of the vehicle are provided in the section on the simulations. The effectiveness of the developed method has been demonstrated using the MATLAB/CarSim joint simulation platform. There are no additional data or materials associated with this study.
Financial support and sponsorship
This work was supported in part by National Key R & D Program of China under Grant No: 2020AAA0108100; in part by Shanghai Natural Science Foundation under Grant No: 21ZR1482300 and 19ZR1461400; and in part by the Fundamental Research Funds for the Central Universities.
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2022.
REFERENCES
1. Hasenjäger M, Heckmann M, Wersing H. A survey of personalization for advanced driver assistance systems. IEEE Trans Intell Veh 2020;5:335-44.
2. Li L, Wen D, Zheng N, Shen L. Cognitive cars: a new frontier for ADAS research. IEEE Trans Intell Trans Syst 2012;13:395-407.
3. Muresan MP, Nedevschi S. Multimodal sparse LIDAR object tracking in clutter. In: 2018 IEEE 14th International Conference on Intelligent Computer Communication and Processing (ICCP); 2018. pp. 215–21.
4. Cheng J, Ju M, Zhou M, Liu C, Gao S, et al. A dynamic evolution method for autonomous vehicle groups in a highway scene. IEEE Int Things J 2022;9:1445-57.
5. Yuan T, Krishnan K, Duraisamy B, Maile M, Schwarz T. Extended object tracking using IMM approach for a real-world vehicle sensor fusion system. In: 2017 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI); 2017. pp. 638–43.
6. Guo C, Meguro J, Kojima Y, Naito T. A multimodal ADAS system for unmarked urban scenarios based on road context understanding. IEEE Trans Intell Transp Syst 2015;16:1690-704.
7. Hosseinnia SH, Tejado I, Milanés V, Villagrá J, Vinagre BM. Experimental application of hybrid fractional-order adaptive cruise control at low speed. IEEE Trans Contr Syst Techn 2014;22:2329-36.
8. Wang X, Chen M, Zhu M, Tremont P. Development of a kinematic-based forward collision warning algorithm using an advanced driving simulator. IEEE Trans Intell Trans Syst 2016;17:2583-91.
9. Pananurak W, Thanok S, Parnichkun M. Adaptive cruise control for an intelligent vehicle. In: 2008 IEEE International Conference on Robotics and Biomimetics; 2009. pp. 1794–99.
10. Asadi B, Vahidi A. Predictive cruise control: utilizing upcoming traffic signal information for improving fuel economy and reducing trip time. IEEE Trans Contr Syst Techn 2011;19:707-14.
11. Chiang HH, Wu SJ, Perng JW, Wu BF, Lee TT. The human-in-the-loop design approach to the longitudinal automation system for an intelligent vehicle. IEEE Trans Syst, Man, Cybern - Part A: Syst Humans 2010;40:708-20.
12. Akhegaonkar S, Nouvelière L, Glaser S, Holzmann F. Smart and green ACC: energy and safety optimization strategies for EVs. IEEE Trans Syst, Man, Cybern: Syst 2018;48:142-53.
13. Li S, Li K, Rajamani R, Wang J. Model Predictive Multi-Objective Vehicular Adaptive Cruise Control. IEEE Trans Contr Syst Technol 2011;19:556-66.
14. Hu J, Zhu J, Lei G, Platt G, Dorrell DG. Multi-objective model-predictive control for high-power converters. IEEE Trans Energy Conv 2013;28:652-63.
15. Bageshwar VL, Garrard WL, Rajamani R. Model predictive control of transitional maneuvers for adaptive cruise control vehicles. IEEE Trans Veh Technol 2004;53:1573-85.
16. Li SE, Jia Z, Li K, Cheng B. Fast online computation of a model predictive controller and its application to fuel economy–oriented adaptive cruise control. IEEE Trans Intell Trans Syst 2015;16:1199-209.
17. Corona D, De Schutter B. Adaptive cruise control for a SMART car: a comparison benchmark for MPC-PWA control methods. IEEE Trans Contr Syst Techn 2008;16:365-72.
18. Moser D, Schmied R, Waschl H, del Re L. Flexible spacing adaptive cruise control using stochastic model predictive control. IEEE Trans Contr Syst Techn 2018;26:114-27.
19. Li SE, Guo Q, Xu S, Duan J, Li S, et al. Performance enhanced predictive control for adaptive cruise control system considering road elevation information. IEEE Trans Intell Veh 2017;2:150-60.
20. Gao B, Cai K, Qu T, Hu Y, Chen H. Personalized adaptive cruise control based on online driving style recognition technology and model predictive control. IEEE Trans Veh Techn 2020;69:12482-96.
21. Yang D, Zong G, Su SF.
22. Xie X, Wei C, Gu Z, Shi K. Relaxed resilient fuzzy stabilization of discrete-time Takagi-Sugeno systems via a higher order time-variant balanced matrix method. IEEE Trans Fuzzy Syst 2022:1-1.
23. Yang W, Feng G, Zhang T. Robust model predictive control for discrete-time Takagi–sugeno fuzzy systems with structured uncertainties and persistent disturbances. IEEE Trans Fuzzy Syst 2014;22:1213-28.
24. Nguyen AT, Taniguchi T, Eciolaza L, Campos V, Palhares R, et al. Fuzzy control systems: past, present and future. IEEE Comput Intell Mag 2019;14:56-68.
25. Nguyen AT, Rath J, Guerra TM, Palhares R, Zhang H. Robust set-invariance based fuzzy output tracking control for vehicle autonomous driving under uncertain lateral forces and steering constraints. IEEE Trans Intell Transp Syst 2021;22:5849-60.
26. Zhang C, Lam HK, Qiu J, Qi P, Chen Q. Fuzzy-model-based output feedback steering control in autonomous driving subject to actuator constraints. IEEE Trans Fuzzy Syst 2021;29:457-70.
27. Nguyen AT, Sentouh C, Zhang H, Popieul JC. Fuzzy static output feedback control for path following of autonomous vehicles with transient performance improvements. IEEE Trans Intell Transp Syst 2020;21:3069-79.
28. Zhang D, Wang J. A curving ACC system with coordination control of longitudinal car-following and lateral stability. Veh Syst Dyn 2012;50:1085-102.
29. Liu F, Chen Y. Improved model predictive control for cooperative adaptive cruise control subject to actuator delay. In: 2017 Chinese Automation Congress (CAC); 2017. pp. 4747–22.
30. Zhang H, Zhang X, Wang J. Robust gain-scheduling energy-to-peak control of vehicle lateral dynamics stabilisation. Veh Syst Dyn 2014;52:309-40.
31. Baffet G, Charara A, Dherbomez G. An observer of tire–road forces and friction for active security vehicle systems. IEEE/ASME Trans Mechatr 2007;12:651-61.
32. Rajamani R. Vehicle dynamics and control. Springer Science & Business Media; 2011.
33. Nguyen A, Sentouh C, Zhang H, Popieul J. Fuzzy static output feedback control for path following of autonomous vehicles with transient performance improvements. IEEE Trans Intell Transp Syst 2020;21:3069-79.
34. Yang W, Gao J, Feng G, Zhang TJ. An optimal approach to output-feedback robust model predictive control of LPV systems with disturbances. Int J Rob Nonl Contr 2016:26.
35. Jiang ZP, Wang Y. Input-to-state stability for discrete-time nonlinear systems. Automatica 2001;37:857-69.
36. Magni L, Raimondo DM, Scattolini R. Regional input-to-state stability for nonlinear model predictive control. IEEE Trans Autom Contr 2006;51:1548-53.
37. Xie L, Fu M, de Souza CE. H/sub infinity/control and quadratic stabilization of systems with parameter uncertainty via output feedback. IEEE Trans Autom Contr 1992;37:1253-56.
38. Kothare MV, Balakrishnan V, Morari M. Robust constrained model predictive control using linear matrix inequalities. Automatica 1996;32:1361-79.
40. Cheng S, Li L, Guo H, Chen Z, Song P. Longitudinal collision avoidance and lateral stability adaptive control system based on MPC of autonomous vehicles. IEEE Trans Intell Trans Syst 2020;21:2376-85.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Zhang C, Wei X, Wang Z, Zhang H, Guo X. T-S fuzzy-model-based adaptive cruise control for longitudinal car-following considering vehicle lateral stability. Intell Robot 2022;2(4):371-90. http://dx.doi.org/10.20517/ir.2022.26
AMA Style
Zhang C, Wei X, Wang Z, Zhang H, Guo X. T-S fuzzy-model-based adaptive cruise control for longitudinal car-following considering vehicle lateral stability. Intelligence & Robotics. 2022; 2(4): 371-90. http://dx.doi.org/10.20517/ir.2022.26
Chicago/Turabian Style
Zhang, Changzhu, Xiaoyu Wei, Zhuping Wang, Hao Zhang, Xuyang Guo. 2022. "T-S fuzzy-model-based adaptive cruise control for longitudinal car-following considering vehicle lateral stability" Intelligence & Robotics. 2, no.4: 371-90. http://dx.doi.org/10.20517/ir.2022.26
ACS Style
Zhang, C.; Wei X.; Wang Z.; Zhang H.; Guo X. T-S fuzzy-model-based adaptive cruise control for longitudinal car-following considering vehicle lateral stability. Intell. Robot. 2022, 2, 371-90. http://dx.doi.org/10.20517/ir.2022.26
About This Article
Copyright
Data & Comments
Data

 Cite This Article 11 clicks
Cite This Article 11 clicks












Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.