Stability compensation of an admittance-controlled cartesian robot considering physical interaction with a human operator
Abstract
In human-machine systems, admittance control is widely used for controlling robots. However, the problem with this method is that the stability can be impacted by the stiffness of the machine and the human operator. In order to minimize the oscillation issue that is caused by insufficient structure stiffness, this study used compensation methods, specifically feed-forward and acceleration feedback. Simulation results show that both compensation methods can expand the stability region of the system. Nevertheless, feedback compensation is more appropriate than feed-forward when taking into account uncertainties in the structure parameters of the system. Even when the system is not perfectly implemented, feedback compensation can keep the system stable, whereas feed-forward compensation causes a significantly reduced stability region. From the experiment, it is also confirmed that the feedback system has an advantage over the feed-forward system, and this simple feedback using an accelerometer can compensate for the insufficient stiffness of the robot structure and greatly enhance the stability of the human-machine system.
Keywords
1. INTRODUCTION
Robots are created to perform tasks more efficiently and accurately than human operators. In situations that are too dangerous or inaccessible for humans, deploying robots can provide a safer and more effective solution. However, in order to make a robot perform tasks, instructions must be given. While simple robot movements can be controlled with buttons, joysticks, or computer codes, tracing human movement while they perform difficult tasks is challenging. Another solution is to use a human–robot collaboration system, which enables direct interaction between human operators and robots[1–3]. In particular, power-assist systems and direct robot teaching are examples of applications for such systems in which human operators and robots physically interact[4]. In such systems, human operators will be able to guide the movements of a robot at will. To realize such systems, the robot must be properly controlled based on the manipulation force of the operator.
Admittance control is one method to realize such a system[5]. A human-machine system can be a closed-loop system consisting of an admittance-controlled robot and a human operator. Interaction forces are generated by end-effectors that are touched by humans, measured by force sensors, and input into the admittance model. However, admittance control has the disadvantage that the stability of the system is affected by the stiffness of the environment, the time delay of the control, and the bandwidth of the actuator[6,7]. In human-machine systems, the stiffness of the human and the stiffness of the structure of a robot are particularly important[8]. When human stiffness increases, to prevent robots from oscillating, the admittance model must be changed by increasing the viscosity and mass parameters[9]. Several variable admittance control methods have been proposed to improve operability[10], but the variable parameter range is limited to maintain stability[11–15]. If the structural characteristics of the original robot system have a large influence, the range of variable parameters will be narrow, and the improvement in operability will be limited. Especially in the case of cartesian robots, where the mass of the movable actuator is large, the force required to move that actuator itself is greater, so the effect of insufficient structural stiffness of the robot is greater. This requires a particularly large mass parameter in the admittance model to ensure stability, resulting in poor maneuverability.
In this study, we focused on improving the stability of the human-machine system without decreasing the admittance characteristic of the system. The idea is to make a compensator that can reduce the effect of structural characteristics that affect system stability to a minimum. Buerger et al. propose a method for designing an actuator controller for an interactive robot with structural resonance[16]. This approach is similar to ours, as it uses a feedback controller to compensate for the structural characteristics of the robot and shape the open-loop characteristics to improve stability. However, it assumes force control of the actuator and is difficult to incorporate into admittance control, which is position-based impedance control. Therefore, we propose a new method to compensate for the structural characteristics of the robot that can be easily applied to admittance control.
To design a compensator for use in the system, we have to know the characteristics of the robot, which consist of an actuator system and structural characteristics, which can be obtained through a spectrum analysis experiment[17]. After that, a compensator can be designed to achieve a wider stability range in operation. Therefore, we can use lower inertia and viscosity parameters in the admittance model, which means the operator can work in a lighter environment and extend the operation duration before starting to get tired. We consider feed-forward and feedback compensators. Feed-forward compensators are simple and require no extra sensors, but they are not robust to changes in the structure characteristics. In contrast, feedback compensators are robust but require sensors to measure the motion of the structure. Motion sensors on actuators (typically rotary encoders, etc.) are relatively internal sensors and cannot measure absolute motion, which is important for interaction with the operator outside the robot. In this study, the absolute motion of the structure is measured by accelerometers that can be easily attached to the structure of the robot.
The results from simulations show that by appending feed-forward and feedback compensation, they can expand the stability region by a significant amount. However, the stability region of a feed-forward compensated system will easily decrease if the structure characteristic of the actual system is not the same as the measurement. Therefore, we designed a feedback compensated system to overcome this limitation. With feedback compensation, the system can maintain the stability region even if the structure characteristics change from our measurement.
Experiments are carried out to test the improvement of the compensated systems. The results show that both systems can stably operate with a higher admittance characteristic, indicated by a lower mass parameter, compared to the uncompensated system. And also, feedback compensation can operate at a lower mass parameter in the admittance model compared to feed-forward compensation, which means feedback compensation is more robust and preferable in practical application.
2. ADMITTANCE CONTROL OF THE HUMAN-INTERACTIVE ROBOT
2.1. Admittance control
The admittance control is a way to control robots with human interaction; control input to the system will come from the applied force of human operators, and the robot will move according to the admittance model to the desired position. Admittance is the inverse of impedance, and an impedance model is a transfer function that receives position information and calculates force output; therefore, an admittance model will receive force input information,
Figure 1. Block diagram of an admittance control robot, where
We consider the mass spring damper system as an admittance model. However, in our study, it does not need to return to the origin after the operator breaks the contact, so the stiffness parameter can be neglected. The transfer function of the admittance model,
2.2. Human-machine system
The robot requires instructions to move according to the needs of the human operator. The admittance control method is used when control is input via human-robot interaction. As shown in Figure 2, a robot that makes contact with the operator forms a single-couple system, and human interaction creates a closed-loop system[5]. The impedance of the human operator,
Closed-loop systems can have instability problems that also depend on
3. MODELING
3.1. Experiment setup
The experiment setup shown in Figure 3 is designed for a power-assisted robot system. It is equipped with a force sensor, AC servo motors, servo packs, and linear sliders. A laser distance sensor is used for only spectrum analysis, and an acceleration sensor is used for feedback compensation mentioned later. These devices are connected to a PC, as shown in Figure 4, to form the experiment setup, where the PC performs measurements, calculates control operations, and outputs position command pulses to the servo packs with a sampling time of 1 ms.
3.1.1. Force sensor
A Force sensor is a device used to measure the applied force and sends out digital data to the computer. In this experiment, the force/torque sensor from Nitta was used, and its specifications are shown in Table 1.
Force sensor specification
| Force sensor | |
| Manufacture | Nitta |
| Model | IFS-50M31A25-I25 |
| Rated Input Force (XY) | 100 N |
| Rated Input Force (Z) | 200 N |
| Rated Input Torque (XYZ) | 5 Nm |
3.1.2. Servo packs & AC servo motors
Servo packs and AC servo motors are devices that work together. Servo packs supply electrical power to an AC servo motor, and the motor feeds feedback data from an encoder attached to its end to the servo pack, which detects the current position and adjusts the electrical power so that the AC servo motors turn to the correct position. Tables 2 and 3 show the specifications of the servo packs and AC servo motors used in the experiment.
Servo packs specification
| Servo packs | |
| Manufacture | Yaskawa Electric Corporation |
| Model | SGDV-2R8F01A |
AC servo motors specification
| AC servo motors | |
| Manufacture | Yaskawa Electric Corporation |
| Model | SGMJV-04ADA2C |
| Rated Output | 400 W |
| Rated Torque | 1.27 Nm |
| Rated Current | 2.7 Arms |
| Rated Rotational Speed | 3000 rpm |
| Encoder | 20-bit serial encoder (incremental) |
3.1.3. Linear sliders
The servo motor creates rotational motion, but in this experiment, the robot needs to move in horizontal and vertical linear motion; therefore, linear sliders are used to convert rotational motion to linear motion. The specification of the horizontal axis linear slider is shown in Table 4, and the specification of the vertical axis linear slider is shown in Table 5.
Horizontal axis linear slider specification
| Horizontal axis linear slider | |
| Manufacture | NSK |
| Model | MCH10105H20D |
| Nominal Stroke | 1050 mm |
| Ball Screw Lead | 20 mm |
| Mass | 33 kg |
Vertical axis linear slider specification
| Vertical axis linear slider | |
| Manufacture | NSK |
| Model | MCH10100H20K |
| Nominal Stroke | 1110 mm |
| Ball Screw Lead | 20 mm |
| Mass | 27 kg |
3.1.4. Laser distance sensor
For spectrum analysis, structure displacement must be measured. Therefore, a laser distance sensor is placed in the system to be used to measure structure displacement that results from oscillation, and its specifications can be found in Table 6.
Laser distance sensor specification
| Laser distance sensor | |
| Manufacture | Panasonic |
| Model | HG-C1030 |
| Output Type | NPN output |
| Measurement Center Distance | 30 mm |
| Measurement Range | |
3.1.5. Acceleration sensor
In subsequent sections, we use the acceleration of the structure of the robot as feedback to the control system, so an acceleration sensor is attached to the frame. Its specifications are listed in Table 7.
Acceleration sensor specification
| Acceleration sensor | |
| Manufacture | Kionix |
| Model | KXR94-2050 |
| Measurement Range | |
| Sensitivity | 660mV/G |
| Frequency Range | 800Hz (-3dB) |
3.2. Modeling
3.2.1. Actuator system transfer function
The actuator system is required to move the robot to the desired coordinate. It consists of servo packs, AC servo motors, and linear sliders, where each component has its own characteristics. In this study, we will represent the characteristic of all these components with one transfer function,
3.2.2. Structure transfer function
From the test bench shown in Figure 3, a structure has an X- and Y-axis actuator in the system, as shown in Figure 5. From our previous research, we found that the X-axis is more unstable compared to the Y-axis when a human operator interacts with the robot. So, in this study, we will concentrate on only the X-axis, which leads to system instability. We consider the horizontal structure movement as a single mass spring damper system in which the parameters are
Absolute displacement of the robot end-effector,
Equations (3 and 4) are created by focusing on all forces applied to each mass; therefore, derived equations will get a transfer function, as shown in Equation (5).
3.3. Spectrum analysis
Spectrum analysis is the process of analyzing a signal in the frequency domain, which reveals the frequencies and their associated magnitudes and phases that are present in the signal. This can be used to identify frequency components within a signal. In this study, Spectrum analysis is used for creating a Bode diagram of a system using input and output signals that are measured from the test system.
The fast Fourier transform algorithm is a widely used method for spectrum analysis that can calculate the discrete Fourier transform of a given signal. However, this algorithm is unsuitable for analyzing noise signals that are random and stochastic because it does not have well-defined frequencies. To analyze noise signals, power spectral analysis is a more suitable method. It can estimate the power of a signal at each frequency. But this method is still for analyzing a single signal. A cross-power spectral density, an extension of power spectral analysis, can give the result of total noise power spectral density in complex values at each frequency and is used to analyze the correlation between two signals.
The cross-correlation method is used to find the amplitude and frequency relationship between two signals. It can be expressed as Equation (6), where
The cross-power spectral density is the Fourier transformation of cross-correlation as Equation (8). For finite discrete-time signals, it can be mathematically expressed as Equation (9). In this study, the
The transfer function can be estimated using the cross-power spectral density of the input and output signals, as shown in Equation (10), and the magnitude and angle of the complex number results will yield the transfer function amplitude and phase.
In this experiment, white noise is generated and used as the input of the system. and the output of the system consists of actuator displacement from the rotary encoder attached to the servo motor and structure displacement from the laser distance sensor, as shown in Figure 7. This data will be used to determine the actuator system and structure characteristics.
Actuator displacement,
The actuator system receives control system signal input,
Resulting constants were
4. STABILITY ANALYSIS
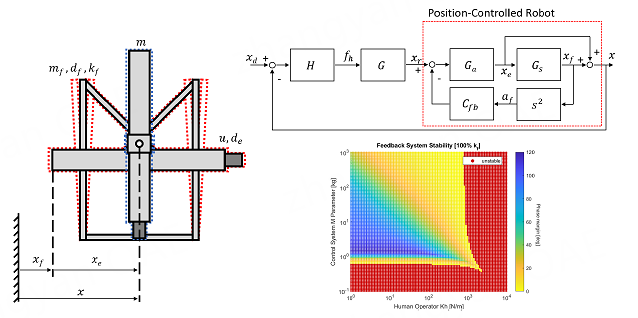
4.1. Block diagram and transfer function of human-machine system
To analyze the stability of the experiment system, including the human operator, we need to consider the block diagram, as shown in FFigure 12. The human operator impedance,
Due to the insufficient stiffness of the robot, structure displacement that is created by robot movement has to be considered, so the absolute end-effector position,
As a result, we can express the overall transfer function,
4.2. Stability margin
Phase margin is a method used to check the stability of the feedback system. It measures how much phase shift can be applied before the system becomes unstable. To check the stability of a feedback system, we have to determine the open loop transfer function of the system and then find the gain crossover frequency, which is the point where the gain is unity. If the phase at that point is greater than
When the system is in contact with a human operator, it might become unstable. The harder the operator grabs the end-effector, the more the system will oscillate, and the impedance of the operator,
In this section, we simulated system stability with changes in
According to the results in Figure 13, the system is unstable until the damping coefficient exceeds around
Moving on to Figures 16-18, it is shown that changing the value of the damping parameter,
Figures 16-18 also show that to maintain system stability, the stiffness of the human operator,
5. FEED-FORWARD COMPENSATION
5.1. Design
A feed-forward compensator is a control system component that is used to improve the performance of the system. As shown in Figure 19, the compensator is inserted in series with the control system. In this study, we tried to minimize the effect of structure characteristics by adding a simple compensator to the system. The compensator,
In Figure 20, the Bode diagram shows the response of the overall robot transfer function,
5.2. Simulation
The compensator that is applied to the system is the inverse of the structure transfer function, so we have to consider the error of the structure parameter measurement because if the measurement is not exactly the same as the actual system, the designed compensator will not cancel out the structure transfer function. With this situation, we also need to consider that the actual system has a different natural frequency from the measurement, and the parameter that directly changes natural frequency is the stiffness of the structure and the mass of the structure. In this simulation, we consider the change in structure stiffness,
Figure 21. Feed-forward system stability analysis with actual system structure stiffness at
Figure 22. Feed-forward system stability analysis with actual system structure stiffness at
Figure 23. Feed-forward system stability analysis with actual system structure stiffness at
From Figure 21, when the compensator perfectly cancels out the structure characteristic, the stability region is increased compared to the system without compensation shown in Figure 16. It shows that a feed-forward compensator allows us to use a smaller
To easily compare the stability region between an uncompensated and a feed-forward system, we display the stability boundary of both simulations in the same graph, as shown in Figure 24 for a perfectly compensated system and Figure 25 for a system considered to have a
Figure 24. Stability region boundary comparison between a non-compensated system and a feed-forward system at
5.3. Experiment
In this experiment, we use the admittance model parameter as follows:
The result in Figure 26 shows that appending a feed-forward compensator to the system can improve the stability of the system. At
6. FEEDBACK COMPENSATION
6.1. Design
A feedback compensator or feedback controller is a control system that will measure the output signal of the system and adjust the input signal to the system. Compared between the feed-forward and feedback compensators, both will improve the performance of the system, but the advantage of the feedback system is that it tends to have better robustness, which means it can maintain performance despite changes in the environment.
As shown in Figure 27, it is a feedback control system in this study, and we use acceleration as the feedback signal because directly measuring absolute structure displacement is not easy in a practice situation. Therefore, we use an accelerometer, which can easily be attached to the frame. The downside of an accelerometer is that it cannot accurately measure a low frequency, but it can be used in this study because we consider only the oscillation frequency range. In Figure 27, the block of
To get better robustness to the change in structure characteristics, we need to make sensitivity small around the resonance frequency. The sensitivity of this system can be calculated using Equation (15).
The experiment system with a feedback controller, which can be expressed in Figure 27, can be derived into Equation (16). To find the sensitivity of the system, we must derivate Equation
We need to design the compensator,
In Equation (18),
Similarly,
Equation (21) shows that if
But in reality, we know that
Because of unstable
Finally, we can replace
Parameters
In Figure 30, the Bode diagram shows the response of the overall robot transfer function,
6.2. Simulation
The simulation is conducted using the same method as a feed-forward compensator simulation. Simulation with an actual system that has exactly the same stiffness as the measurement, as shown in Figure 31, the simulation with an actual system that has stiffness
Figure 31. Feedback system stability analysis with actual system structure stiffness at
Figure 33. Feedback system stability analysis with actual system structure stiffness at
Figure 31 shows that the stability region is improved over a non-compensated system, but it is still smaller than the stability region achieved with feed-forward compensation, as shown in Figure 21. However, when the actual system structure stiffness decreases from measurement by
In Figure 34, it is shown that when the compensator is perfectly canceling out structure characteristics in feed-forward compensation, it has an advantage in the stability region over the feedback system. But when the system is not perfectly compensated, as shown in Figure 35, it shows that the feedback system can remain stable with little change, but the stability region of the feed-forward system reduces significantly to the point that the feedback system has a greater stability region than the feed-forward system.
Figure 34. Stability region boundary comparison between a non-compensated system, a feed-forward system, and a feedback system at
6.3. Experiment
In the experiment, we use the admittance model parameter as follows:
From Figure 36, it is clear that a feedback compensator can greatly improve the stability of the system compared to a non-compensated system. However, Figure 36 also shows that the feedback system has low-frequency movement when a human operator is in contact with the machine, and it causes movement when the human operator attempts to make the end-effector remain in the same position. The damping parameter,
Figure 36. Non-compensated system and feedback system stability experiment with
And when comparing feed-forward compensation with feedback compensation, as shown in Figure 37, feedback compensation has a slight improvement in stability over feed-forward compensation in this condition, so we try another experiment with a smaller
Figure 37. Feed-forward system and feedback system stability experiment with
Figure 38. Feed-forward system and feedback system stability experiment
Figure 38 shows that in a feed-forward system, it cannot remain stable even when a human operator is not in contact with it, and it starts to aggressively oscillate when a human is in contact at
Figure 37 and Figure 38 show that when we change parameter
7. CONCLUSION
In this study, we know that the human-machine system will face an unstable situation when a human operator is in contact with the machine when the stiffness of the structure is not high enough. Therefore, we have two methods of adding a compensator to the system that helps improve the stability region of the human-machine system, so we can use a lighter weight in the admittance model, which means the operator can work in a lighter load environment.
The first one is a feed-forward compensator, which uses the inverse of the structure transfer function to cancel out structure characteristics that cause oscillations. The simulation section shows that the stability region is greatly improved over an uncompensated system, and we can use a lower
With feed-forward compensation, the stability region is greatly reduced by the difference between the measurement and the actual parameter. So, we tried a feedback compensator with an accelerometer, which is another method to compensate for structure characteristics. Although in simulation, it shows that the stability region is not improved from an uncompensated system as much as a feed-forward system. However, we consider conditions when a structure parameter is different from what we measure. It shows that the feedback system is greatly improved over the feed-forward system, and it can remain stable when actual structure parameters change. From the experiment, it is also confirmed that the feedback system has an advantage over the feed-forward system, with
Furthermore, we plan to refine the admittance model design because we know that the stability of the system also depends on human interaction, which causes differences in each movement due to changes in human impedance, so we will use a dynamic variable in the admittance model. It will be changed according to human movement and task so the operator can move the object with a light force during a traveling task and can perform a high-precision task when needed. The feedback compensation studied in this study should increase the range of variation in the admittance model.
DECLARATIONS
Authors' contributions
Conducted the experiment, simulation, data acquisition, and data analysis: Songthumjitti N
Conceived and designed the study: Inaba T
Interpreted the results: Songthumjitti N, Inaba T
Availability of data and materials
Not applicable.
Financial support and sponsorship
None.
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2023.
REFERENCES
1. Villani V, Pini F, Leali F, Secchi C. Survey on human-robot collaboration in industrial settings: safety, intuitive interfaces and applications. Mechatronics 2018;55:248-66.
2. Matheson E, Minto R, Zampieri EGG, Faccio M, Rosati G. Human-robot collaboration in manufacturing applications: a review. Robotics 2019;8:100.
3. Hentout A, Aouache M, Maoudj A, Akli I. Human-robot interaction in industrial collaborative robotics: a literature review of the decade 2008 - 2017. Advanced Robotics 2019;33:764-99.
4. Krüger J, Lien T, Verl A. Cooperation of human and machines in assembly lines. CIRP Annals 2009;58:628-46.
5. Keemink AQ, van der Kooij H, Stienen AH. Admittance control for physical human-robot interaction. Int J Rob Res 2018;37:1421-44.
6. Lawrence DA. Impedance control stability properties in common implementations. In: Proceedings. 1988 IEEE International Conference on Robotics and Automation; 1988. p. 1185-90.
7. Tsumugiwa T, Yokogawa R, Yoshida K. Stability analysis for impedance control of robot for human-robot cooperative task system. In: Proceedings of 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); 2004. p. 3883-8.
8. Calanca A, Muradore R, Fiorini P. A review of algorithms for compliant control of stiff and fixed-compliance robots. IEEE/ASME Trans Mechatron 2016;21:613-24.
9. Tsumugiwa T, Fuchikami Y, Kamiyoshi A, Yokogawa R, Yoshida K. Stability analysis for impedance control of robot in human-robot cooperative task system. J Adv Mech Des Systs Manufacturing 2007;1:113-21.
10. Sharkawy A, Koustoumpardis PN. Human-robot interaction: a review and analysis on variable admittance control, safety, and perspectives. Machines 2022;10:591.
11. Kang G, Oh HS, Seo JK, Kim U, Choi HR. Variable admittance control of robot manipulators based on human intention. IEEE/ASME Trans Mechatron 2019;24:1023-32.
12. Lecours A, Mayer-St-Onge B, Gosselin C. Variable admittance control of a four-degree-of-freedom intelligent assist device. In: 2012 IEEE International Conference on Robotics and Automation; 2012. p. 3903-8.
13. Dimeas F. Online stability in human-robot cooperation with admittance control. IEEE Trans Haptics 2016;9:267-78.
14. Ferraguti F, Talignani Landi C, Sabattini L, Bonfè M, Fantuzzi C, Secchi C. A variable admittance control strategy for stable physical human - robot interaction. Int J Rob Res 2019;38:747-65.
15. Müller F, Janetzky J, Behrnd U, Jäkel J, Thomas U. User force-dependent variable impedance control in human-robot interaction. In: 2018 IEEE 14th International Conference on Automation Science and Engineering (CASE); 2018. p. 1328-35.
16. Buerger SP, Hogan N. Complementary stability and loop shaping for improved human-robot interaction. IEEE Trans Robot 2007;23:232-44.
17. Narawich SONGTHUMJITTI, Takeshi INABA, Modeling and stability analysis of an admittance-controlled cartesian robot considering physical interaction with humans. In: The 23rd Conference of The System Integration Division, The Society of Instrument and Control Engineering, 3P3-E18 (2022).
18. Inaba T, Shu U. Control of power assist system for easy positioning consideration to maneuverability depending on task direction and operator's posture. IEEJ Trans EIS 2014;134:1130-7.
19. Inaba T, Matsuo Y. Loop-shaping characteristics of a human operator in a force reflective manual control system. In: Systems, Man, and Cybernetics, 1997. Computational Cybernetics and Simulation, 1997 IEEE International Conference on. IEEE, 1995.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Songthumjitti N, Inaba T. Stability compensation of an admittance-controlled cartesian robot considering physical interaction with a human operator. Intell Robot 2023;3(3):306-36. http://dx.doi.org/10.20517/ir.2023.20
AMA Style
Songthumjitti N, Inaba T. Stability compensation of an admittance-controlled cartesian robot considering physical interaction with a human operator. Intelligence & Robotics. 2023; 3(3): 306-36. http://dx.doi.org/10.20517/ir.2023.20
Chicago/Turabian Style
Songthumjitti, Narawich, Takeshi Inaba. 2023. "Stability compensation of an admittance-controlled cartesian robot considering physical interaction with a human operator" Intelligence & Robotics. 3, no.3: 306-36. http://dx.doi.org/10.20517/ir.2023.20
ACS Style
Songthumjitti, N.; Inaba T. Stability compensation of an admittance-controlled cartesian robot considering physical interaction with a human operator. Intell. Robot. 2023, 3, 306-36. http://dx.doi.org/10.20517/ir.2023.20
About This Article
Special Issue
Copyright
Data & Comments
Data
 Cite This Article 13 clicks
Cite This Article 13 clicks


















































Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.